Radiação na Atmosfera

• Prof. Breno Imbiriba
• Periodo especial da PANDEMIA - 2021
• Capítulo 1 - Grandezas Radiométricas

Radiação Eletromagnética

Campos e propagação

• Descoberta por Maxwell - (equações de Maxwell do Eletromagnetísmo)
• Onda formada de campos elétricos e magnéticos.
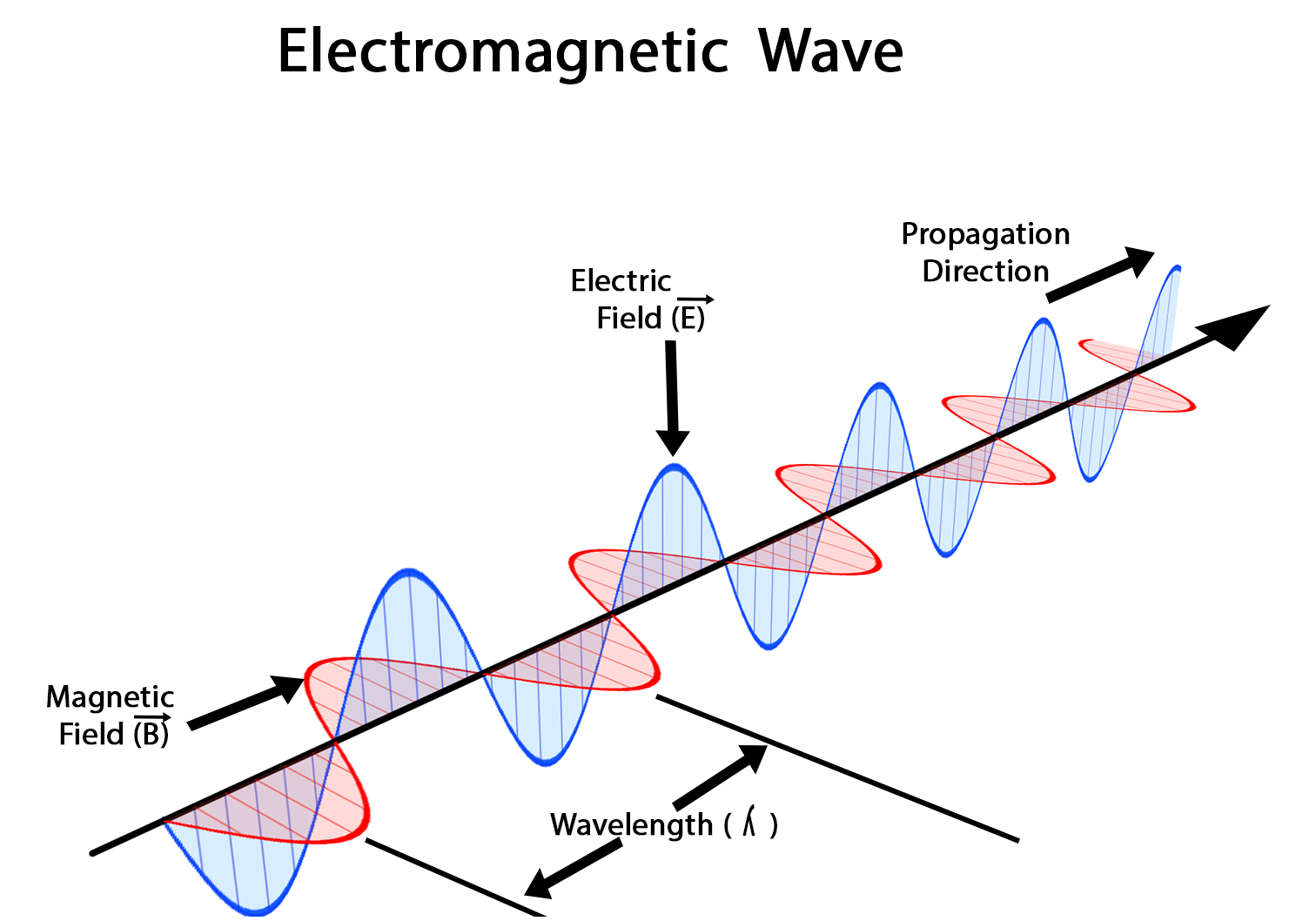
• Propagam-se com a MESMA velocidade: \(c=299,8\) mil km/s.

Radiação Eletromagnética

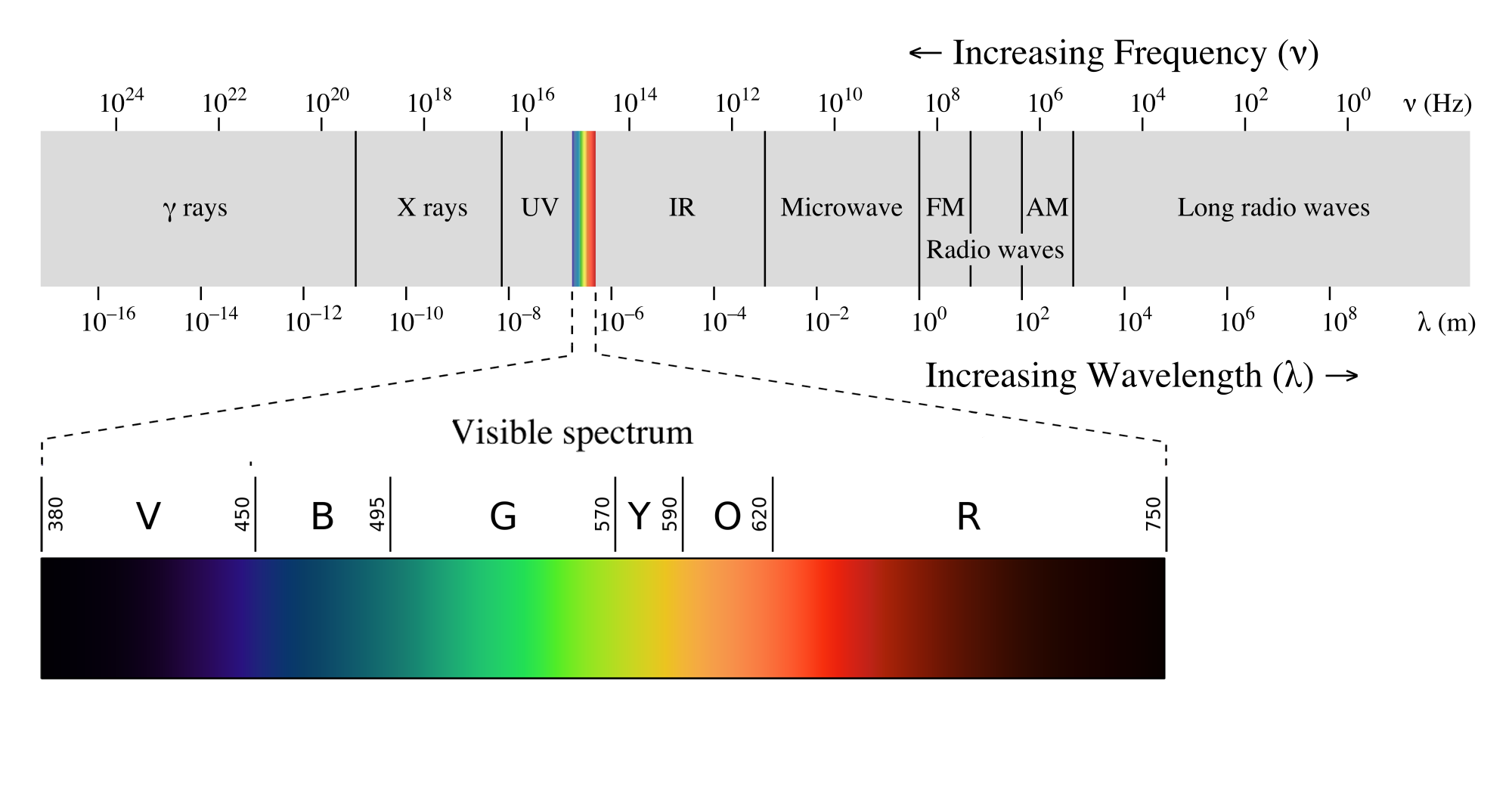
Espectro Eletromagnético

• Radiação Eletromagnética unifica diversos fenômenos:
• Luz, Infravermelho, Ultravioleta, Ondas de Rádio, Microondas, Raios X, Raios Gama.
• Todos são Radiação Eletromagnética - mudando apenas a frequência!!

Radiação Eletromagnética

Quanta de Luz - Na virada do Século XIX para XX:

• Descobriu-se (Planck) que a Energia da luz estava ligada a sua frequência:

\[ E = \frac{hc}{\lambda} = h \nu,\] onde \(h=6,626\times 10^{-34}\)Js, \(\lambda\) é o comprimento de onda (m), \(\nu\) é a frequência (Hz), e \(c\) é a velocidade da luz \(c=299,8\) mil km/s = \(2,998x10^8\)m/s (decorar: 300 mil kilômetros por segundo!).

• Einstein explicou o Efeito Fotoelétrico.

• Unidades comuns para \(\lambda\): mm (rádio), \(\mu\)m (microondas-IV), nm (visível-UV).

Radiação Eletromagnética

Divisão do Espéctro:

• UVC (100-280nm)
• UVB (280-315nm)
• UVA (315-400nm)
• Visível (400-700nm)
• IV próximo (0,78-3,5)\(\mu\)m
• IV termal (3,5\(\mu\)m-1mm)
• Radiação Solar abrange TODO o espéctro, no entanto é mais intenso no visível e UV, indo a zero para \(\lambda > 4\mu\)m.

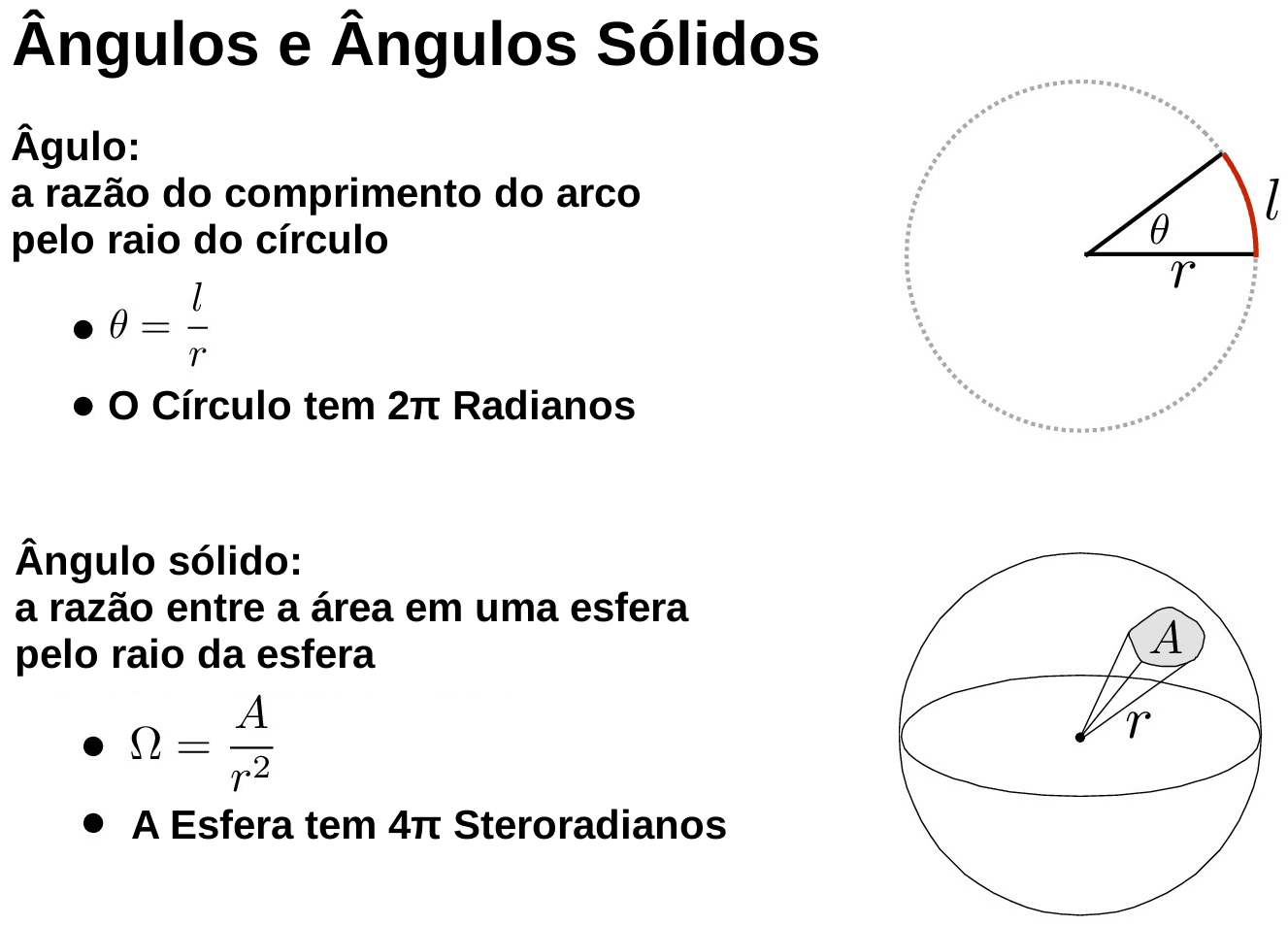
Ângulo Sólido

O que é

• Unidade: steroradiano (sr).

Ângulo Sólido

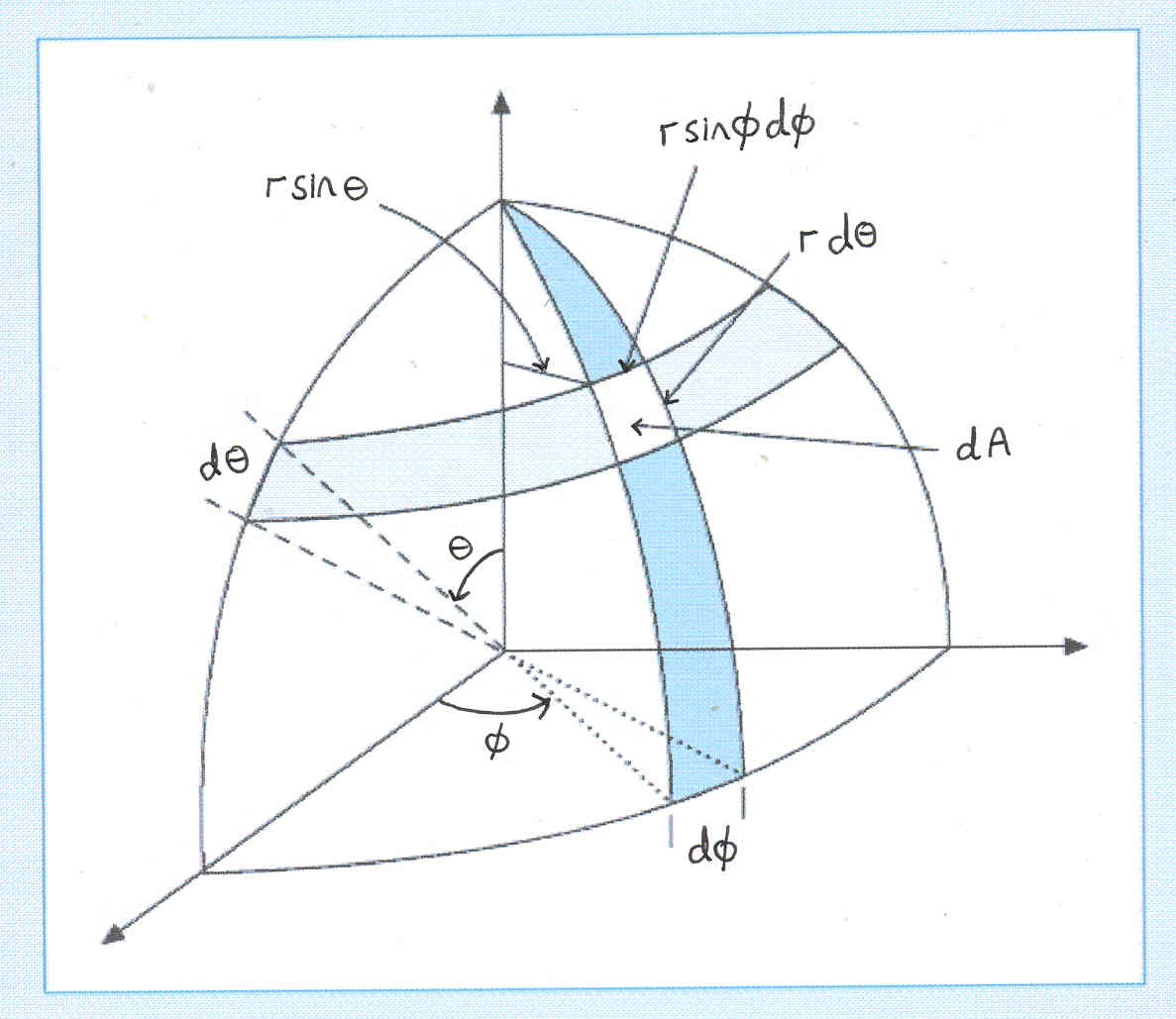
Coordenadas esféricas

• Área de uma calota infinitesimal: \(d\sigma = (r d\theta) (r \sin(\theta) d\phi)\).

Ângulo Sólido

• Assim, a área elementar (infinitesimal) é \(d\sigma = r^2\sin(\theta) d\theta d\phi\).
• O ângulo sólido elementar correspondente é:
  • Ângulo sólido: \(\Omega=\frac{S}{R^2} = \sin(\theta) d\theta d\phi\).

Se estivernos usando latitude e longitude, isto é equivalente à:

• Ângulo sólido: \(\Omega=\frac{S}{R^2} = \cos(lat) dlat\,dlon\).

Ex. Qual é o ângulo sólido de um pequen retângulo de 1 grau por 1 grau? Como não estamos fazendo distinção entre os graus, eles encontram-se no equador de uma esfera imaginária, (\(\theta=90\) ou latitude=0), e assim temos que \(\Delta \Omega \approx (1^\circ)^2 = (\pi/180)^2=.0003\)sr.

Fluxo, Intensidade, Irradiância e Radiância

Fluxo

Definição: Quantidade de energia radiante total liberada por segundo.

• Fluxo de energia = energia dispendida por segundo (potência) \[ \phi = \frac{Q}{T} = \frac{\Delta Q}{\Delta t}= \frac{dQ}{dt}.\]
• \(Q\) - energia radiante (J).
• \(\phi\) - fluxo de energia (W).
• \(T\) - tempo considerado (s).

Ex. Uma lâmpada incandescente de potência de 60W têm como fluxo de energia os mesmos \(\phi=60\)W. Ela emite 60J por segundo de energia radiante. (No caso da lâmpada incandescente, a maior parte desta energia é no infravermelho térmico).

Fluxo, Intensidade, Irradiância e Radiância

Intensidade Radiante

Definição: A potência radiante por unidade de ângulo sólido emitida por uma fonte puntual.

• De uma fonte puntual em uma determinada direção:
• O fluxo de energia dividido pelo ângulo sólido de propagação dessa radiação: \[ I=\frac{\phi}{\Omega} = \frac{\Delta\phi}{\Delta\Omega}= \frac{d\phi}{d\Omega}.\]

Ex. Na mesma lâmpada de 60W, se ela emite em todas as direções igualmente, podemos dizer que a intensidade é \[I = 60/4\pi = 4,77\text{W/sr}.\]

Note: A Intensidade \(I\) pode se referir tanto a energia de sai de uma fonte, quanto à intensidade que atinge um observador.

Fluxo, Intensidade, Irradiância e Radiância

Irradiância

Definição: Potência radiante que atinge uma determinada área.

• Em um determinada area em uma superfície: \[ E=\frac{\Delta\phi}{\Delta A}=\frac{d\phi}{dA}.\]

• Ex. A radiação solar atinge a superfície da Terra com irradiância de \(1,3\mathrm{kW/m}^2\).

Fluxo, Intensidade, Irradiância e Radiância

Radiância

Definição: Fluxo radiante em uma superfície, por ângulo sólido e por área projetada (na direção da radiação).

• Radiância emitida: \(A\) é a área da fonte e \(\Omega\) é o ângulo sólido da emissão.
• Radiância recebida: \(A\) é a área do detector e \(\Omega\) é o ângulo sólido da fonte vista pelo detector.
• Área projetada: \(A\cos(\theta)\), \(\theta\) = ângulo com a normal.

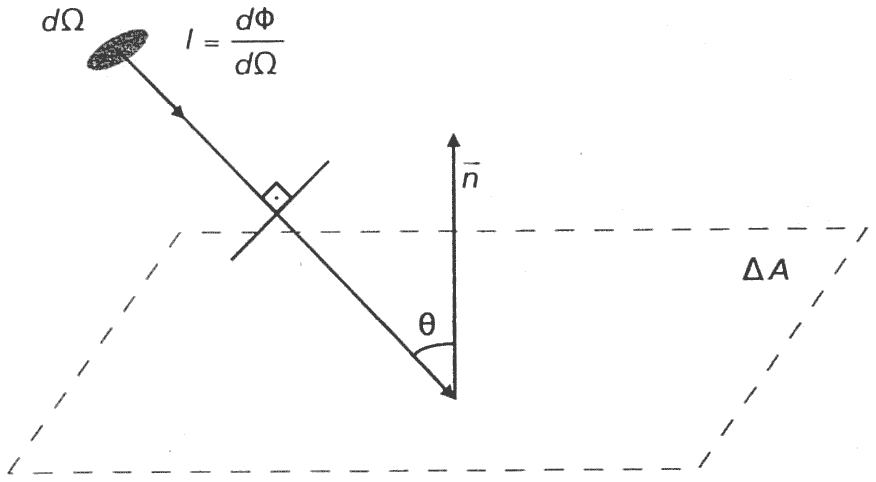
Fluxo, Intensidade, Irradiância e Radiância

• Em uma dada direção, em um dado ponto (área) de uma superfície:
• A razão entre a intensidade radiante emitida pela área ortogonal insidente: \[ L=\frac{1}{\cos{\theta}}\frac{\Delta I}{\Delta A}=\frac{1}{\cos{\theta}}\frac{dI}{dA} = \frac{1}{\cos{\theta}}\frac{d^2\phi}{dAd\Omega}.\]
• Ou a razão da Irradiância pelo ângulo sólido: \[ L=\frac{1}{\cos{\theta}}\frac{\Delta E}{\Delta \Omega}=\frac{1}{\cos{\theta}}\frac{dE}{d\Omega}.\]

Fluxo, Intensidade, Irradiância e Radiância

Fluxo, Intensidade, Irradiância e Radiância

Radiância - Irradiância

• Outra maneira de definir Irradiância
• Integral da radiância (L) pelo ângulo sólido: \[ E = \int L \cos{\theta} d\Omega = \int_{\theta_i}^{\theta_f} \int_{\phi_i}^{\phi_f} L \cos{\theta} \sin{\theta}d\theta d\phi.\]

Para a esfera total: \[ E = \int_S L \cos{\theta} d\Omega = \int_{0}^{\pi} \int_{0}^{2\pi} L \cos{\theta} \sin{\theta}d\theta d\phi.\]

Lista de Exercícios 1

1. Calcule a frequencia de oscilação de:
   • Ondas de rádio: \(\lambda=1cm\)
   • Microondas: \(\lambda=1mm\)
   • Infravermelho; \(\lambda=10\mu\)m
   • Visível verde
   • UVA

2. Mostrar que o ângulo sólido de uma esfera é \(4\pi\).

3. Calcule o ângulo sólido de um retângulo de 1°x1° (lat/lon) sobre a superfície da Terra, na linha do equador.

Lista de Exercícios 1 - cont.

4. \(\phi\), I, E, L:
   1. Fluxo \(\phi\): Considere uma lâmpada incandescente de 60W e assuma que toda esta potência seja de energia radiante. Qual é o valor do fluxo de energia radiante \(\phi\)?
   2. Intensidade \(I\): Considerando esta lâmpada como uma fonte de energia radiante puntual, e considerando que ela emita igualmente em todas as direções.
      1. Qual o ângulo sólido \(\Omega\) em que a radiação é emitida? Calcule a intensidade média da radiação \(I\).
      2. Considere que agora que é colocado um espelho metálico plano infinito atrás da lâmpada, efetivamente refletindo toda a sua energia para frente. Qual é o novo ângulo sólido \(\Omega\) no qual a radiação é emitida? Calcule a nova intensidade \(I\).
   3. Irradiância \(E\): Se 2600W de potência atingem uma área de 2m², calcule o valor de \(E\).
   4. Radiância \(L\): O Sol tem irradiância \(I=1300\)W/m². O disco solar ocupa apenas uma pequena porção do céu, em termos de ângulo sólido, apenas 0,00024sr. Assumindo que o Sol esteja a pino (ou seja, faça um ângulo de 0° com a normal), calcule a radiância \(L\).

Lista de Exercícios 1 - cont.

5. A irradiância solar tem um valor de \(1,3\)kW/m\({}^2\). Calcule quanta energia pode ser captada por um painel solar de \(2\mathrm{m}^2\) durante o período de uma hora ao meio dia, assumindo uma eficiência de 30%.

6. Provar que, se a radiação for isotrópica, ou seja, a radiância é a mesma em todas as direções (constante igual a \(L\)), a irradiância total incidente em um hemisfério é igual a \(\pi L\).