Equação da velocidade de uma onda
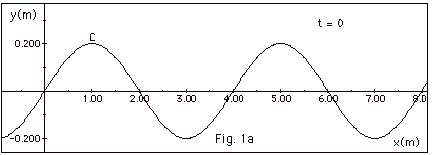
- Senoide: uma onda simples:
- Comprimento (de onda): \(\lambda=4.0\)m.
- Amplitude (a altura): \(A=0.2\)m.
- Mas ondas "andam" (se propagam)
Equação da velocidade de uma onda
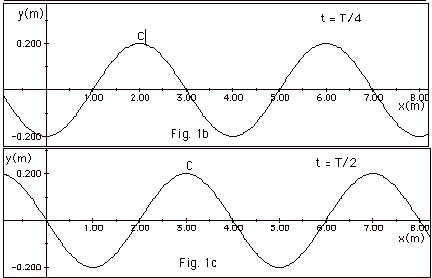
- Andando para a Direita - depois de 0.25s e 0.5s (T=1s):
- Velocidade: \(v=\Delta x/\Delta t = 1/0,25 = 4\text{m/s}\).
Equação da velocidade de uma onda
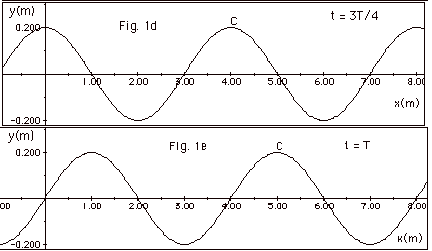
- Andando para a Direita - depois de 0.75 e 1.0s (T=1s):
- Período (Tempo para voltar à forma original): \(T=1\text{s}\).
Equação da velocidade de uma onda
Note o período e velocidade: \(v=\lambda/T = 4/1 = 4\)m/s.
A Frequencia - o inverso do período: \(f=1/T\) em Hertz (1/s).
- Assim: \(v=\lambda f\).
A frequencia \(f\) também é descrito com a letra grega \(\nu\) (ni).
Como fazer uma onda andar? Fase.
- Fase: é o argumento da função seno:
- ex: \(\sin(\pi/4)\), fase \(\phi=\pi/4\).
- ex: \(\sin(45^\circ)\), fase \(\phi=45^\circ\).
- A onda se repete depois de uma mudança de Fase de \(2\pi\).
- Relação posição - Fase (regra de três) \[ \begin{array}{lcr}
\lambda &\rightarrow &2\pi \\
x &\rightarrow&\phi
\end{array}
\]
- A Função para qualquer \(x\) fica então: \[f(x) = A\sin\left(\frac{2\pi}{\lambda} x\right).\]
Como fazer uma onda andar? Tempo.
- Como andar para a DIREITA?
- Uma função \(f(x)\) se desloca para a direita se subtrairmos um valor de \(x\):
- \(f(x-a)\) é a mesma função mas deslocada de \(a\) para a DIREITA.
- A onda anda com uma velocidade \(v\) para a DIREITA. Qual é o deslocamento?
- \(v=\Delta x/\Delta t\), logo: \(\Delta x = v\Delta t\).
- Assim: \[f(x)\rightarrow f(x-\Delta x) = f(x-vt)\]
Como fazer uma onda andar? Tempo.
- Para a onda senoidal: \(v=\lambda f\), logo:
\[
\begin{array}{lcl}
f(x,t) &=& A\sin\left(\frac{2\pi}{\lambda}(x - v t)\right)=\\
&=& A\sin\left(\frac{2\pi}{\lambda}(x - \lambda f t)\right) = \\
&=& A\sin\left(2\pi(\frac{x}{\lambda} - f t)\right).
\end{array}
\]
\[ f(x,t) = A\sin\left(2\pi(kx - \nu t)\right).\]
- \(\nu\) é a frequencia (Hz = 1/s)
- \(k=\frac{1}{\lambda}\) é o número de onda (1/m ou comumente 1/cm ou 1/nm).
Ex. Qual o número de onda de uma onda com \(\lambda=1mm\)? * Quantas ondas cabem em 1cm? Resp = 10. * Então o Número de onda é \(k=10\mathrm{cm}^{-1}\).
Exercícios:
- Calcule o Número de onda de uma onda com \(\lambda=10\mu\)m, \(1\mu\)m e 100nm. Em unidades de 1/cm.
\[ k = \frac{1}{\lambda}. \]
\[ k = \frac{1}{10\times 10^{-6}}\frac{1}{\text{m}} = 10^5 \frac{1}{100\text{cm}} = 1000 \frac{1}{\text{cm}}\]
Note: \[ 10^5 (100\text{cm})^{-1} = 10^5 100^{-1}\text{cm}^{-1} = \frac{10^5}{100}\text{cm}^{-1} = 1000\text{cm}^{-1}.\]
Densidade Espectral
Normalmente a radiação não é monocromática, se espelha em uma região do espéctro. Ex. A radiação de uma lâmpada incandescente abrange tando o visível quanto o infravermelho!
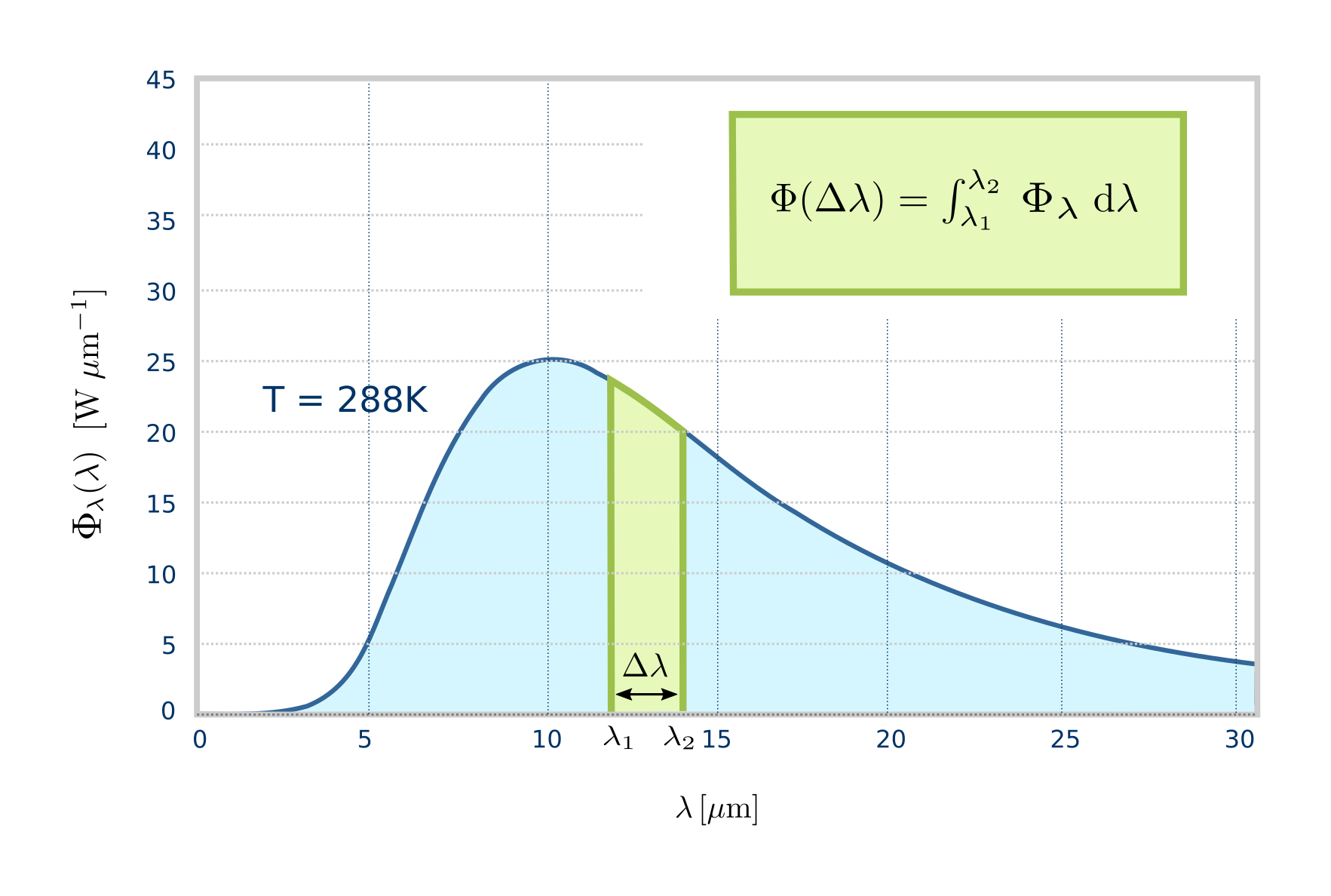
Densidade Espectral: a taxa de radiância emitida por cada comprimento de onda - ou: Considere um comprimento de onda específico \(\lambda_s\), e considere a quantidade de radiância \(\Delta L\) observada mas considerando apenas comprimentos de onda dentro de um intervalo \(\Delta \lambda\) (que contenha \(\lambda_s\)). Assim:
\[ L_\lambda(\lambda_s) = \lim_{\Delta\lambda\rightarrow 0}\frac{\Delta L(\lambda_s)}{\Delta \lambda}=\frac{dL(\lambda_s)}{d\lambda}, \]
Unidades: \(\mathrm{W/m^2/sr/cm}\)
A Radiância total emitida entre num intervalo \(I=[\lambda_1, \lambda_2]\) é
\[ L(\lambda_1,\lambda_2) = \int_{\lambda_1}^{\lambda_2}L_\lambda(\lambda)d\lambda.\]
Densidade Espectral
- A radiância TOTAL (emitida ou absorvida) em todos os comprimentos de onda é dado por:
\[ L_\text{tot} = \int_0^{\infty}\L_\lambda(\lambda)d\lambda. \]
Densidade espectral usando \(\nu\) e k
- A densidade espectral é definida como uma derivada, logo, uma troca de variáveis precisa levar em conta o jacobiano da troca de variáveis:
\[ L_\lambda = \frac{dL}{d\lambda} = \frac{dL}{d\nu}\cdot|\frac{d\nu}{d\lambda}|=L_\nu\cdot|\frac{d\nu}{d\lambda}|.\]
Para calcular o jacobiano, usamos a fórmula: \(c=\lambda\nu\): \[ c = \lambda\nu \rightarrow \nu=c/\lambda\rightarrow \frac{d\nu}{d\lambda} = -\frac{c}{\lambda^2}.\]
- Densidade em termos da frequência: \[L_\nu = \frac{dL}{d\nu} = \frac{dL}{d\lambda} \frac{\lambda^2}{c}.\]
Densidade em termos do número de onda \[L_k = \frac{dL}{dk} = \frac{dL}{d\lambda} \lambda^2.\]
Espalhamento, Absorção e Transmissão
- O fluxo de radiação Eletromagnética (\(\phi\)) incidente na matéria sofre:
- Atenuação: processo de absorção parcial ou total da energia luminosa pela matéria.
- Emissão: processo onde a matéria emite energia radiante aumentando o fluxo.
- Espalhamento: processo onde a luz é redirecionada (para várias direções) pela matéria.
- Esses três processos físicos podem ser resumidos em três parâmetros:
- Absorção: \(\alpha = \frac{\phi_{abs}}{\phi}\).
- Reflexão: \(\rho = \frac{\phi_{refl}}{\phi}\).
- Transmição: \(\tau = \frac{\phi_{trans}}{\phi}\).
- Esses coeficientes são SEMPRE função do comprimento de onda.
Espalhamento, Absorção e Transmissão
- Cada um desse pode acontecer em certa fração:
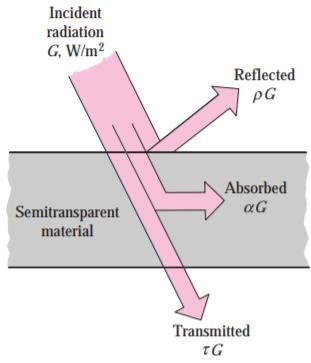
Espalhamento, Absorção e Transmissão
- Absorção da radiação solar como função do comprimento de onda.
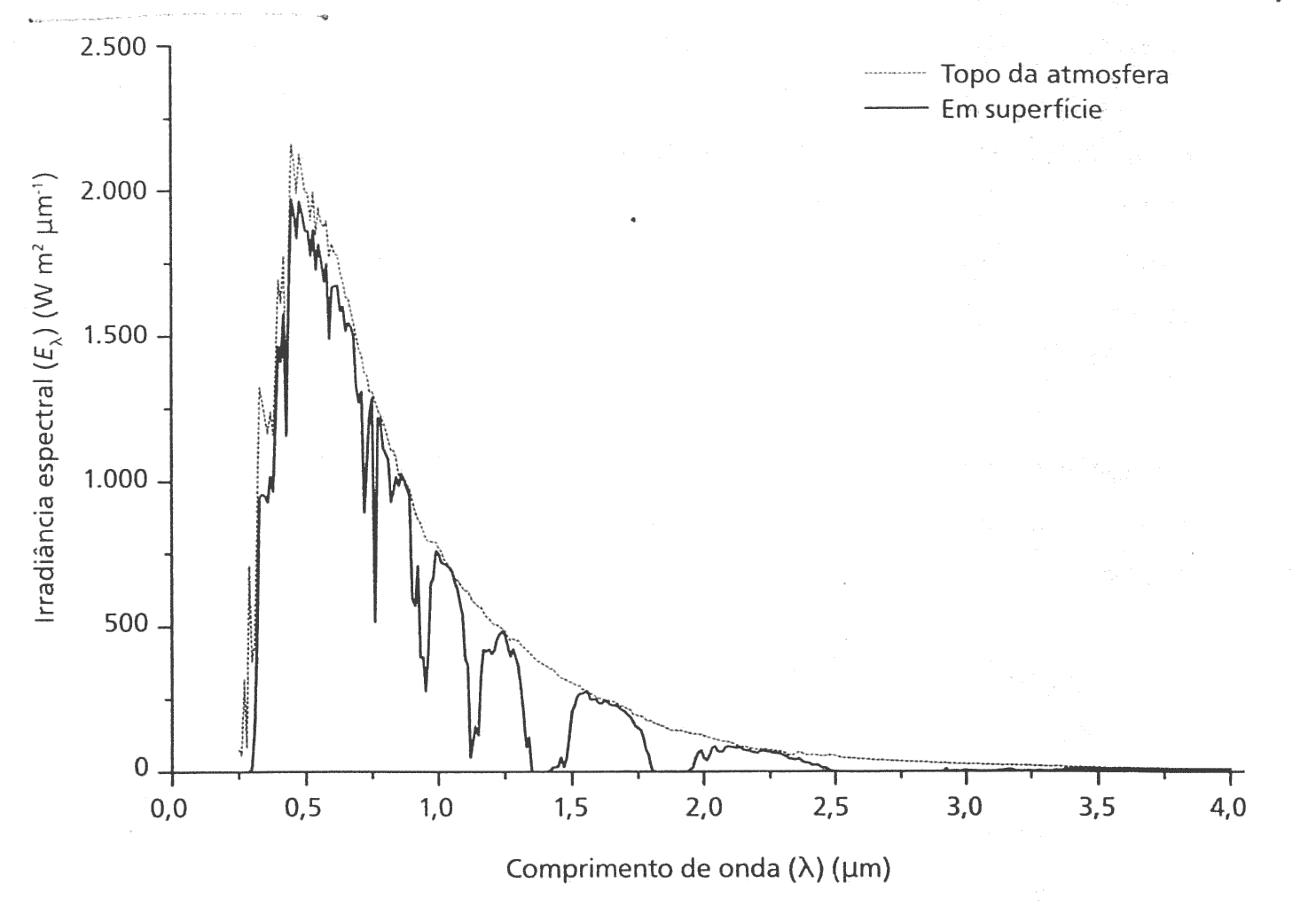
Espalhamento, Absorção e Transmissão
- Por conservação de energia:
- Energia incidente (\(E_{tot}\)) é dividida em três partes (\(E_\rho\), \(E_\tau\), \(E_\alpha\)), ou seja:
\[ E_{tot} = \rho E_{tot} + \tau E_{tot} + \alpha E_{tot},\] ou \[ \rho + \tau + \alpha = 1. \] 
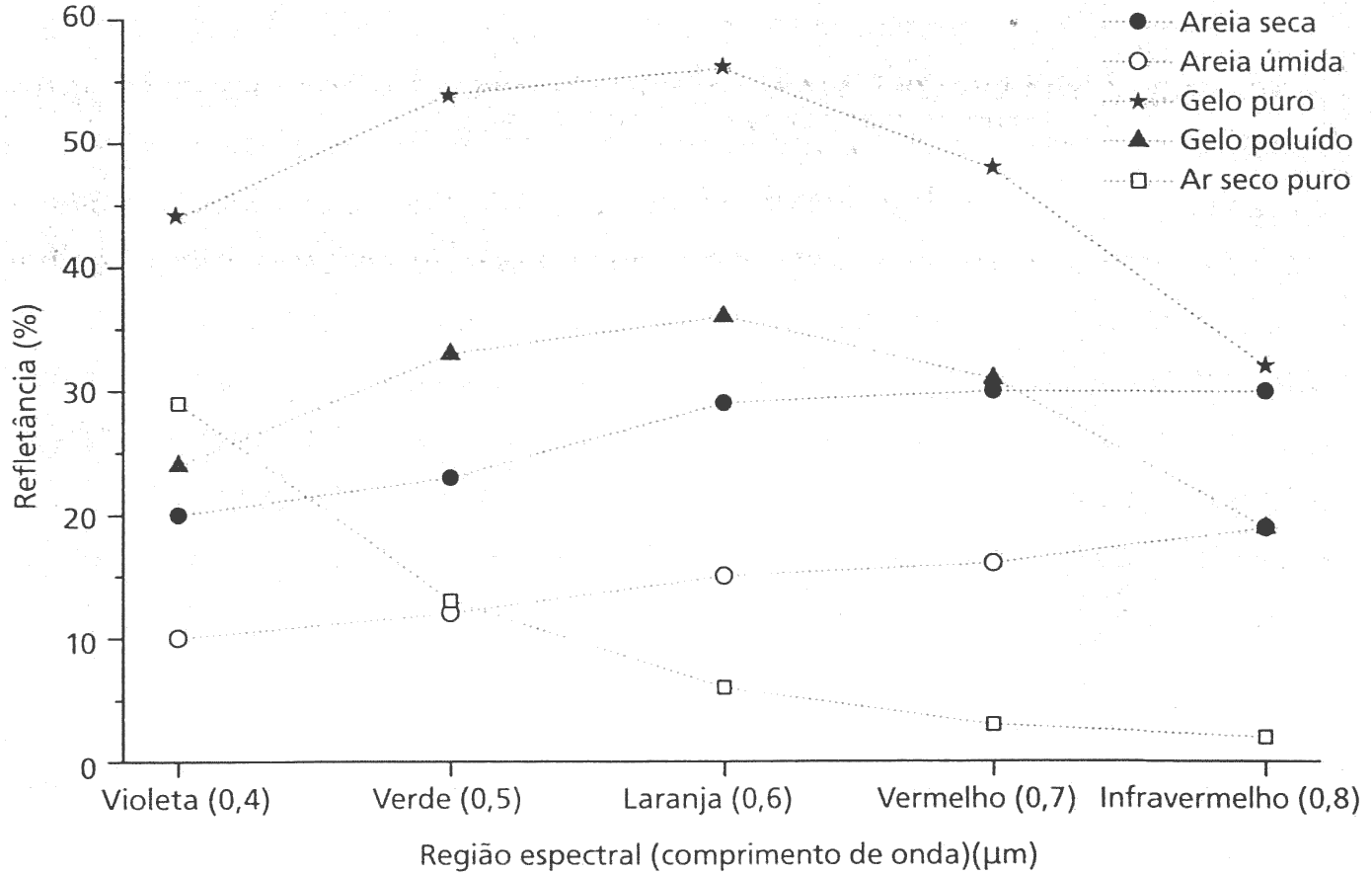
Reflectância - Areia (curtas: \(\lambda<4\mu m\))
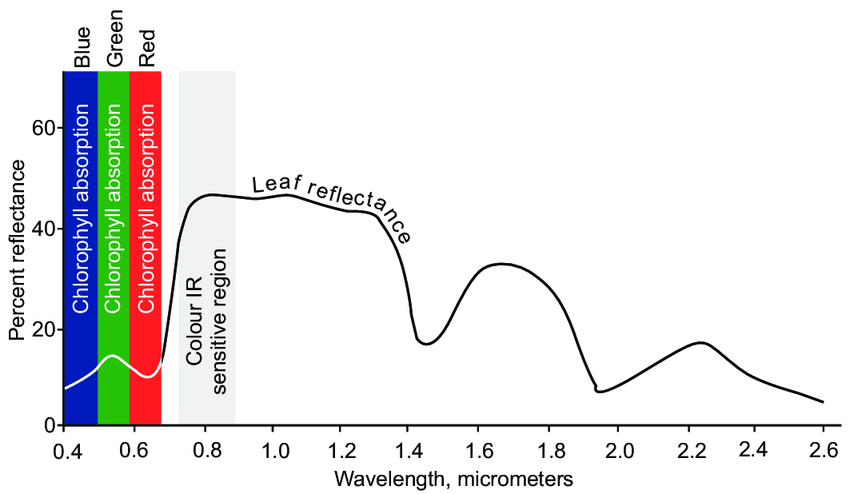
Reflectância - Folha sadia (curtas: \(\lambda<4\mu m\))
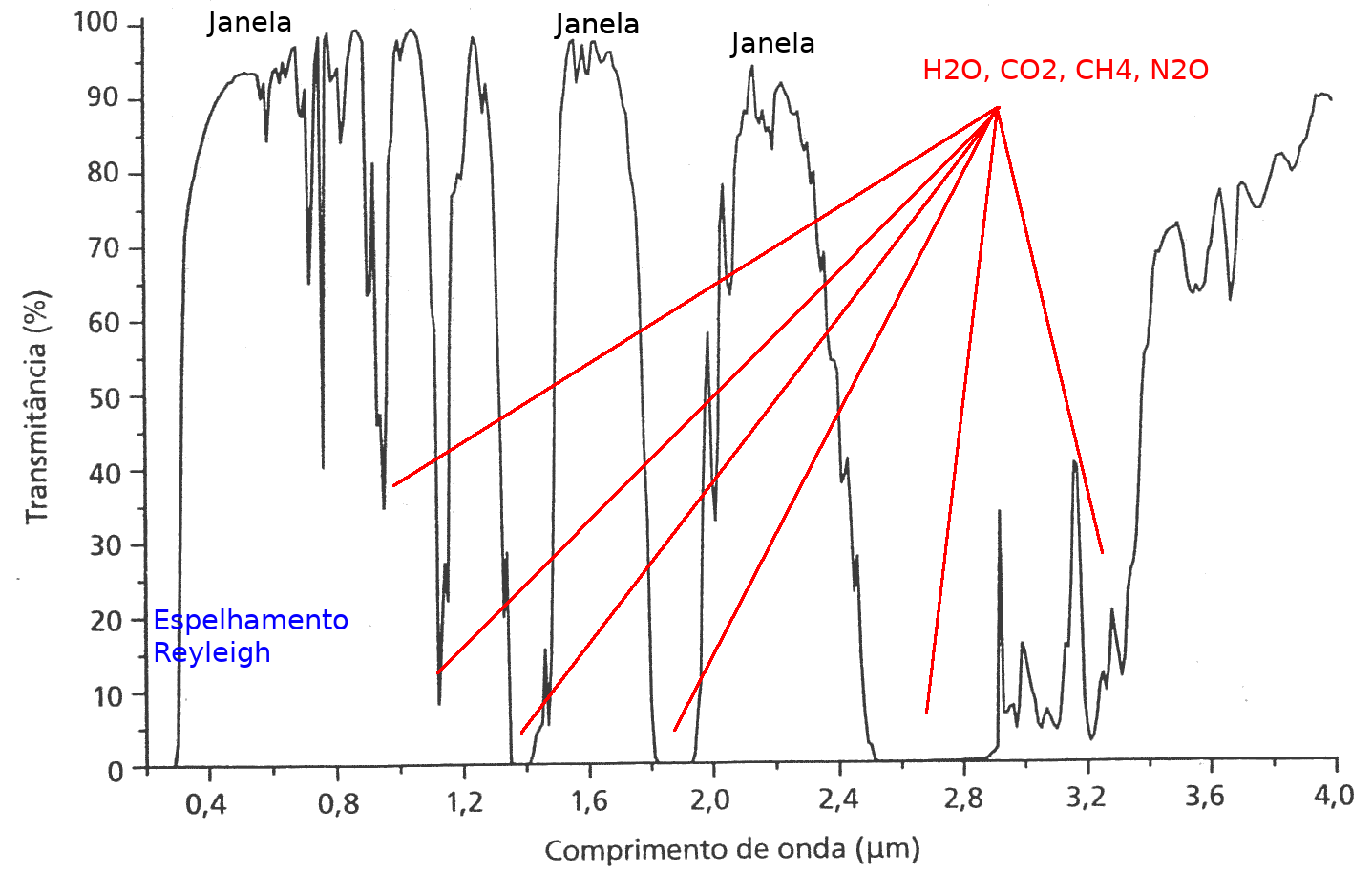
Transmitância - Atmosfera (curta)
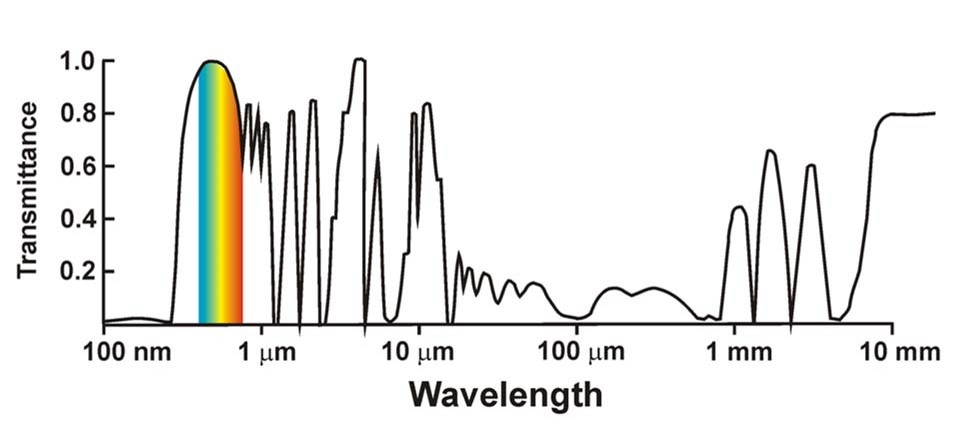
Transmitância - Atmosfera (curta e longa)
Exercícios
Uma folha sadia tem sua reflectância definida como nos slides acima. Calculo o NDVI de uma folha sadia: \[ \mathrm{NDVI} = \frac{|R_{\mathrm{IR}}-R_{\mathrm{RED}}|}{|R_{\mathrm{IR}}+R_{\mathrm{RED}}|}, \] onde RED tem \(\lambda = 700nm\) e IR tem \(\lambda = 1.0 \mu m\).
Imagine que voce tem observações de uma cena onde a luz é separada em cores do espectro. Usando o quadro de reflectância da areia e gelo, como voce poderia distinguir entre os dois? Ou seja, que comparação de cores (e IR) voce poderia usar para disinguir entre eles?