Radiação na Atmosfera

• Prof. Breno Imbiriba
• Periodo especial da PANDEMIA - 2021
• Capítulo 2 - Radiação de Corpo Negro

Radiação de Corpo Negro

• Corpo negro
  • "algo muito preto!"
  • Algo que absorve a 100% da radiação, sem reflexão ou transmissão.
  • Mas o que acontece com a energia absorvida? (imagine o corpo negro como uma um corpo oco com um pequeno furinho)
  
  • A energia fica dentro! \(\rightarrow\) Esquenta! e ai?

Corpo Negro - Lei de Kirchhoff

• Vamos assumir o "Equilíbrio Termodinâmico"
  • (uma maneira bonita de dizer: vamos esperar bastante tempo até que as coisas parem de mudar!)
  • Se está em equilíbrio: \(E_\mathrm{entra} = E_\mathrm{sai}\).
  • Tembém equilíbrio mecânico, quimico, ...
  • Mas de que fora emite energia pra fora? Qual a emissão de energia?
• Um fato da física experimental:
  • Quem absorve bem (reflete pouco, algo escuro) emite bem.
  • Quem absorve mal (reflete muito, algo claro) emite mal.

Lei de Kirchoff

• Lembrando: um corpo absorve radiação, em cada comprimento de onda, de acordo com sua absortância (coeficiente de absorção), \(\alpha_\lambda\).
• A razão entre a energia emitida e o coeficiente de absorção, é uma função universal, \(E_\lambda/\alpha_\lambda=B(\lambda,T)\), que depende apenas de \(\lambda\) da Temperatura do corpo.
• Definindo a Emissividade \(\epsilon_\lambda\) como: \(E_\lambda = \epsilon_\lambda B(\lambda,T)\)
• Lei de Kirchhoff: \[ \epsilon_\lambda = \alpha_\lambda. \]
  • por definição \(\epsilon = 1\) para o Corpo Negro ideal.
  • Tem outros valores para corpos reais.
  • Ainda não sabemos o que é \(B(\lambda, T)\) ainda!

Lei de Kirchoff

• Note:
  • A lei de Kirchhoff vale quano temos Equilíbro Termodinâmico!
  • Em materiais, é necessário haver colisões moleculares suficientes para haver troca de energia.
  • No ar, próximo a superfície, essa troca ocorre rapidamente e diz-se que se está em Equilíbrio termodinâmico.
  • Acima de \(\approx\) 40km de altitude, o ar já se torna bastante rarefeito e neste caso o equilíbrio termodinâmico NÃO OCORRE.
  • Em altas atitude tem-se que se considerar processos radiativos físicos fora do equilíbrio termodinâmico - importante para CO2 na região de 4\(\mu\)m.

Lei de Planck

• Qual é a forma de \(B(\lambda, T)\)?
• Em 1901, Planck tentando encontrar uma expressão para \(B\) notou que:
• Só é possível se a energia for transferida em parcelas fíxas de energia (os quanta de energia)
• \(E = h\nu\), \(h=6,626\times 10^{-34}\)Js, é a constante de Planck.
• A lei de Planck, em função da frequencia \(\nu\) é:

\[ B(\nu,T) = \frac{2h\nu^3}{c^2\left[\exp{\left(h\nu/kT\right)}-1\right]}, \]

em [W/m²/sr/Hz].

Lei de Planck

• Ou, em termos de comprimento de onda: \[ B(\lambda,T) = \frac{2hc^2}{\lambda^5\left[\exp{\left(hc/\lambda kT\right)}-1\right]}, \] em [W/m²/sr/\(\mu\)m].

Lei de Planck - Wein e Stefan-Boltzmann

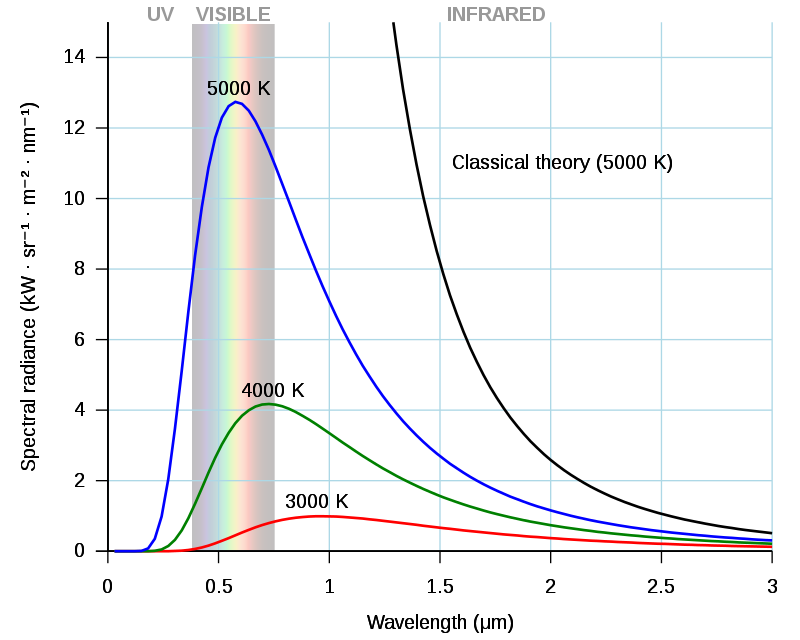
• À partir de Planck, pode-se derivar duas leis que já eram conhecidas antes:

• Wein - o ponto máximo da radiância: \[ \lambda_\mathrm{max} = \frac{2.897}{T}.\]

• Segunda lei de Wein - Radiância máxima: \[ B(\lambda_\mathrm{max},T) = K T^5.\]

• Stefan-Boltzmann - Radiância Total emitida (integrada em todas as frequencias): \[ B(T) = \sigma T^4 = \frac{2\pi^4k^4}{15h^3c^2} T^4, \] onde \(\sigma=5,67\times 10^{-8} \mathrm{W/m^2/K^4}\) é a constante de Stefan-Boltzmann.

• Um corpo REAL tem uma emissividade média \(\epsilon\) e a sua emissão total é: \[E(T) = \epsilon \sigma T^4. \]

Exercícios

1. Obter a expressão da radiância espectral de um corpo negro em função do númedo de onda.

2. Calcular o comprimento de onda de máxima emissão para um ser humano, T=37C, e para o Sol, T=5500C. Em qual banda do espectro encontram-se esses máximos de emissão?

3. Derivar a lei de Wein.

4. Derivar o valor de K na segunda lei de Wein.

Exercícios