Radiação na Atmosfera

• Prof. Breno Imbiriba
• Periodo especial da PANDEMIA - 2020
• Aula 3 - RADIAÇÃO SOLAR - 7/out/2020

O Sol - Características

• A nossa estrela! (amerela)
• Distância média de 150 milhões de kilômetros: \(\bar{d}\approx 149597872km\) = 1 UA (Unidade Astronômica)
  • 1 UA \(\approx 150\times 10^6\)km \(\approx 1,496\times 10^{11}\)m.
  • 1 UA = 8 minutos-luz.

O Sol - Geometria

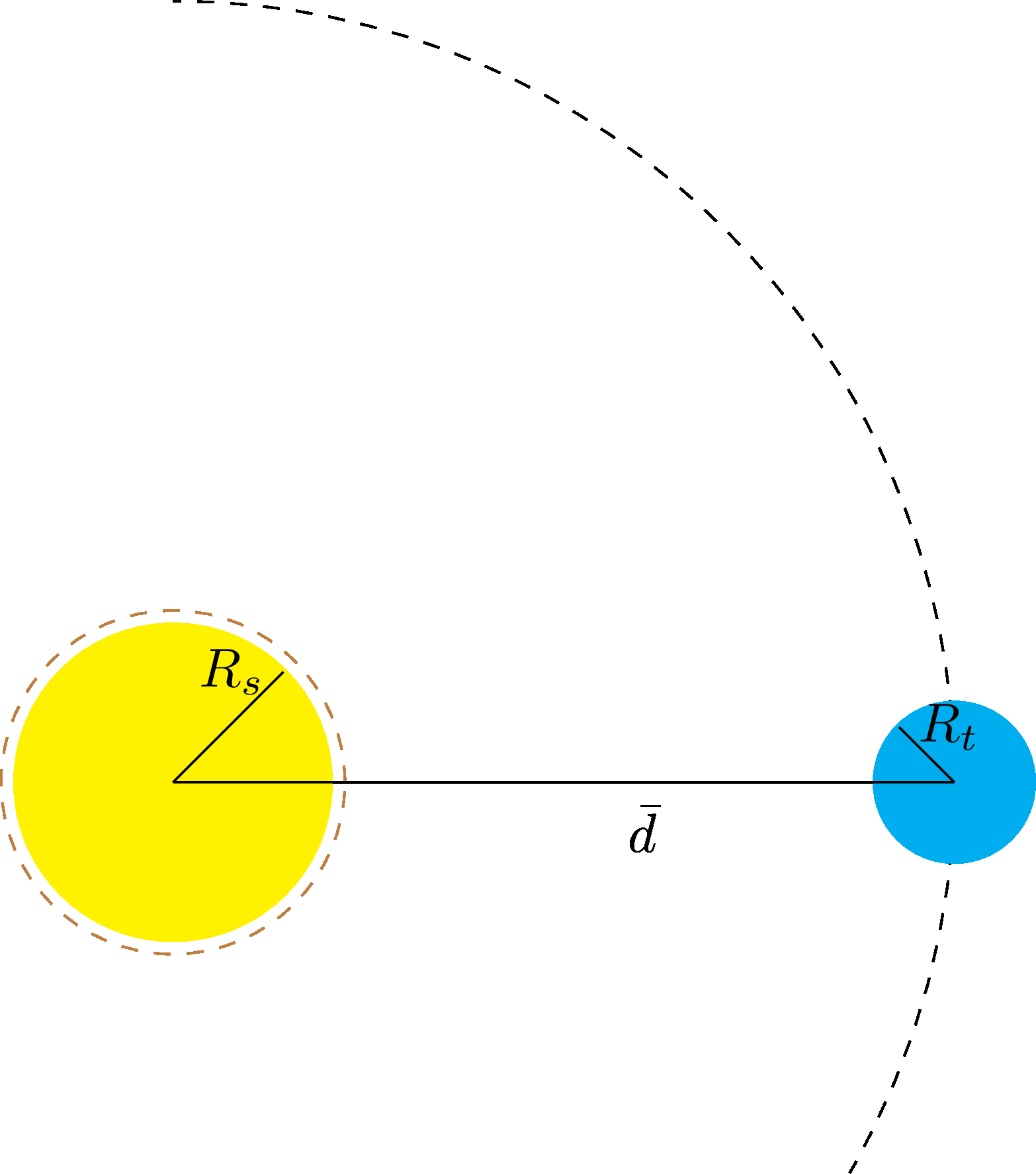
O Sol - Geometria

• Mas a órbita da Terra é elíptica:
  • Periélio \(d=147,1 \times 10^6\)km.
  • Afélio \(d=152,1 \times 10^6\)km.
  • Variação de 3%.
• Forma esferoidal com raio de \(R=696,3\) mil km (a Terra tem raio 6,3 mil km).
• Massa \(M=1,99\times 10^{30}\) kg. (\(M_\mathrm{Terra}=5,97\times 10^{24}\));
  • 75% hidrogênio e hélio, o resto são elementos mais pesados.
  • Energia vinda da fusão nuclear no seu núcleo (Hidrogênio para Hélio, e outros elementos).

O Sol - Radiação

• Empiricamente, chega no planeta Terra (no topo da atmosfera - TOA) a irradiância total solar de: \[ E_0 = 1366 \mathrm{W/m^2},\] chamada constante solar.
  • Essa constante não é bem constante! Varia em cíclos de 11 anos (e outros períodos).
  • Antes das medidas de satélite estimava-se em 1361W/m\({}^2\). (o que é uma questão!!)

O Sol - Manchas solares (histórico)

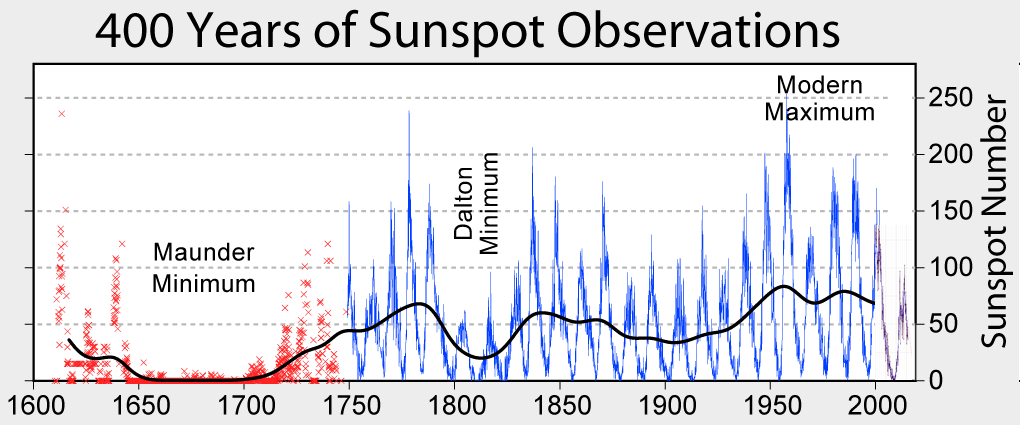
O Sol - Irradiância

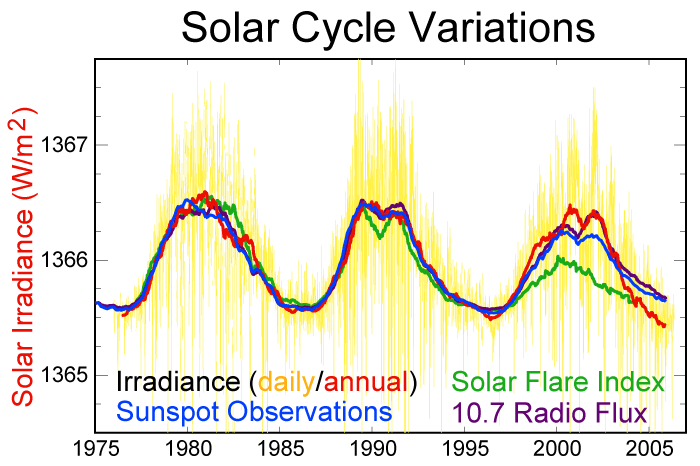
O Sol - Radiação

• Estimativa teórica da constante solar:
  • A Fluxo de Energia (potência) total do Sol: \(\phi_s=3,9\times 10^{26}\)W.
  • A Irradiância Emitida (Pot/Area) é \[E_s=\frac{\phi_s}{A_s}=\frac{\phi_s}{4\pi R_s^2} = \frac{3,9\times 10^{26}}{4\pi(7\times 10^8)^2} = 6,3\times 10^7\mathrm{W/m^2}.\]
  • Essa irradiância total se espalha pelo espaço uniformemente até atingir a Terra, na diatância de 1UA: \[\phi_s=\phi_0\rightarrow E_s4\pi R_s{}^2 = E_04\pi d^2\rightarrow \] \[E_0=\frac{6,3\times 10^7(7\times 10^8)^2}{1,5\times 10^{11})^2} = 1372\mathrm{W/m^2}.\]

O Sol - Radiação

• Como exercício refaça essa conta com os valores mais precisos das variáveis.

• O Sol é aproximadamente um Corpo Negro (Discuta isso!!!)
  • \(T\approx 5800K\)
  • Exercício 1 - Demonstre isso usando a lei de Stefan-Boltzman.

O Sol - Radiação

• Quando a Terra se afasta ou se aproxima do Sol, a irradiância incidente total varia de acordo com: \[E(d) = \left(\frac{\bar{d}}{d}\right)^2E_0.\]
  • Isso é sobre uma superfície PERPENDICULAR aos raios solares (meio-dia!)
  • Exercício 2 - Demonstre essa fórmula.
  • Exercício 3 - Determinar \(E(d)\) para \(d=0,95\bar{d}\) e \(d=1,02\bar{d}\).
  • Exercício 4 - Se a Terra tambem for um corpo negro, estime o valor da sua temperatura nesses dois casos. (use o fato de que a energia que entre na Terra devido ao Sol é a mesma que sai devido a radiação de corpo negro da Terra, dado pela lei de Stefan-Boltzmann.)

O Sol - Radiação

• Problema:
  • No filme “2010” o planeta Jupiter se torna uma estrela. Considere que isso realmente ocorra e ele se torne uma estrela de 6000K. Estime a irradiância total que atingiria a Terra. Assuma que o raio da órbita de Jupite \(R=5,2\)UA, e que o raio de Júpitar seja de 71300km.

O Sol - Radiação

\begin{center} 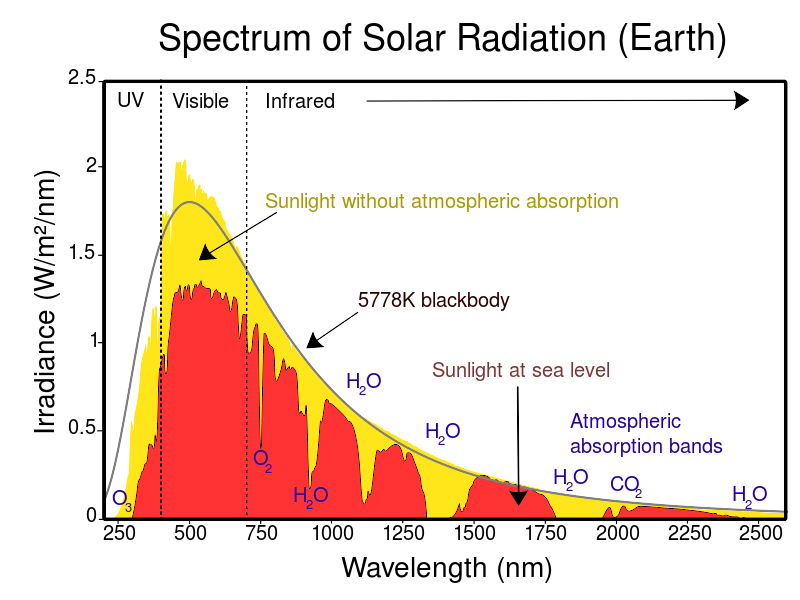\end{center}

Resolução dos exercícios - 1

• Lei de Steffan-Boltzmann: \[ E = \sigma T^4 \mathrm{W/m^2}.\] Nos diz a potência por metro quadrado (irradiância) emitida por um corpo quente.

• Se a irradiância que chega na Terra é de 1366W/m\({}^2\), e o Sol é um corpo-negro, qual é a sua temperatura?
  • Corpo negro: \(E = \sigma T^4\).
  • Na figura, \(\Omega_{sol}=\Omega_{terra}\) logo:
  • A mesma energia que passa em \(\Omega_{sol}\), \(\phi=E_{sol} A_{sol}\) é a mesma que passa em \(\Omega_{terra}\), \(\phi=E_{terra} A_{terra}\). \[\phi_{sol}=\phi_{terra}\rightarrow E_{sol} A_{sol} = E_{terra} A_{terra}.\]

Resolução dos exercícios - 1

• Geometria:

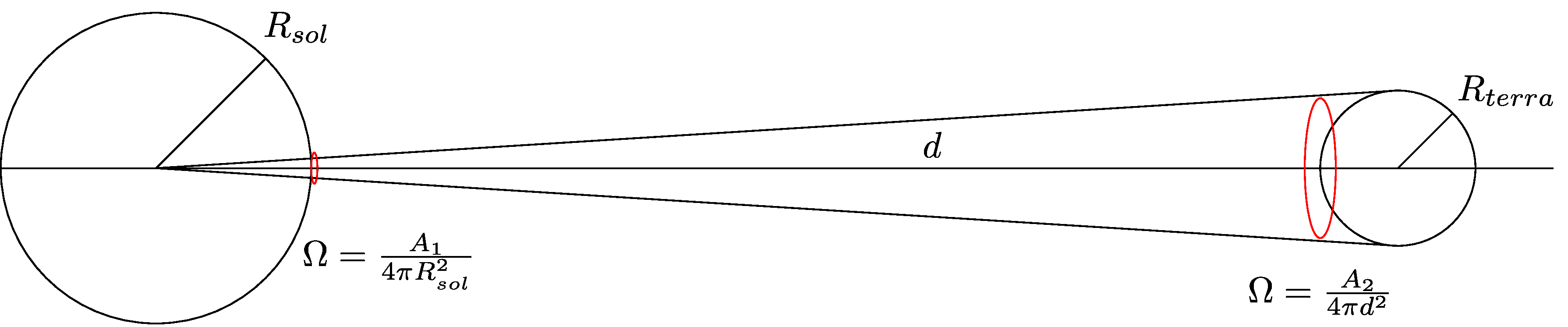
Resolução dos exercícios - 1

• Então
  • Sabemos: \(E_{terra}=1366\mathrm{W/m^2}\),
  • \(A_{terra}=\Omega (4\pi \bar{d}^2)\),
  • \(A_{sol}=\Omega (4\pi R_{sol}^2)\),
  • E resolvemos para \(E_{sol}\). \[E_{sol} = E_{terra} \frac{A_{terra}}{A_{sol}} = 1366\frac{\Omega \bar{d}^2}{\Omega R_{sol}^2}.\]
  • Fazendo a conta: \(E_{sol}=6,305\times 10^7\mathrm{W/m^2} = \sigma T^4\).
  • Calculando: T=5774K.

Resolução dos exercícios - 2

• A irradiância solar é o fluxo total de energia pela área do esfera que envolve o Sol. \[E_0 = \frac{\phi}{4\pi\bar{d}^2}.\]
• Para uma outra distância, basta mudar o valore de \(\bar{d}\).
• Mas o fluxo é sempre constante: \[ \phi=4\pi \bar{d}^2 E_0 = 4\pi d^2 E_d,\] logo \[ E_d = \left(\frac{\bar{d}}{d}\right)^2E_0.\]

Resolução dos exercícios - 3

• Balanço de Energia - O que chega na Terra é o mesmo que Sai. \[\phi_{entra} = \phi_{sai}.\]
• Na Terra chegam 1366W/m2 = \(\sigma T^4\) e teríamos: T=393K - Muito quente!
• Precisa pensar na GEOMETRIA:

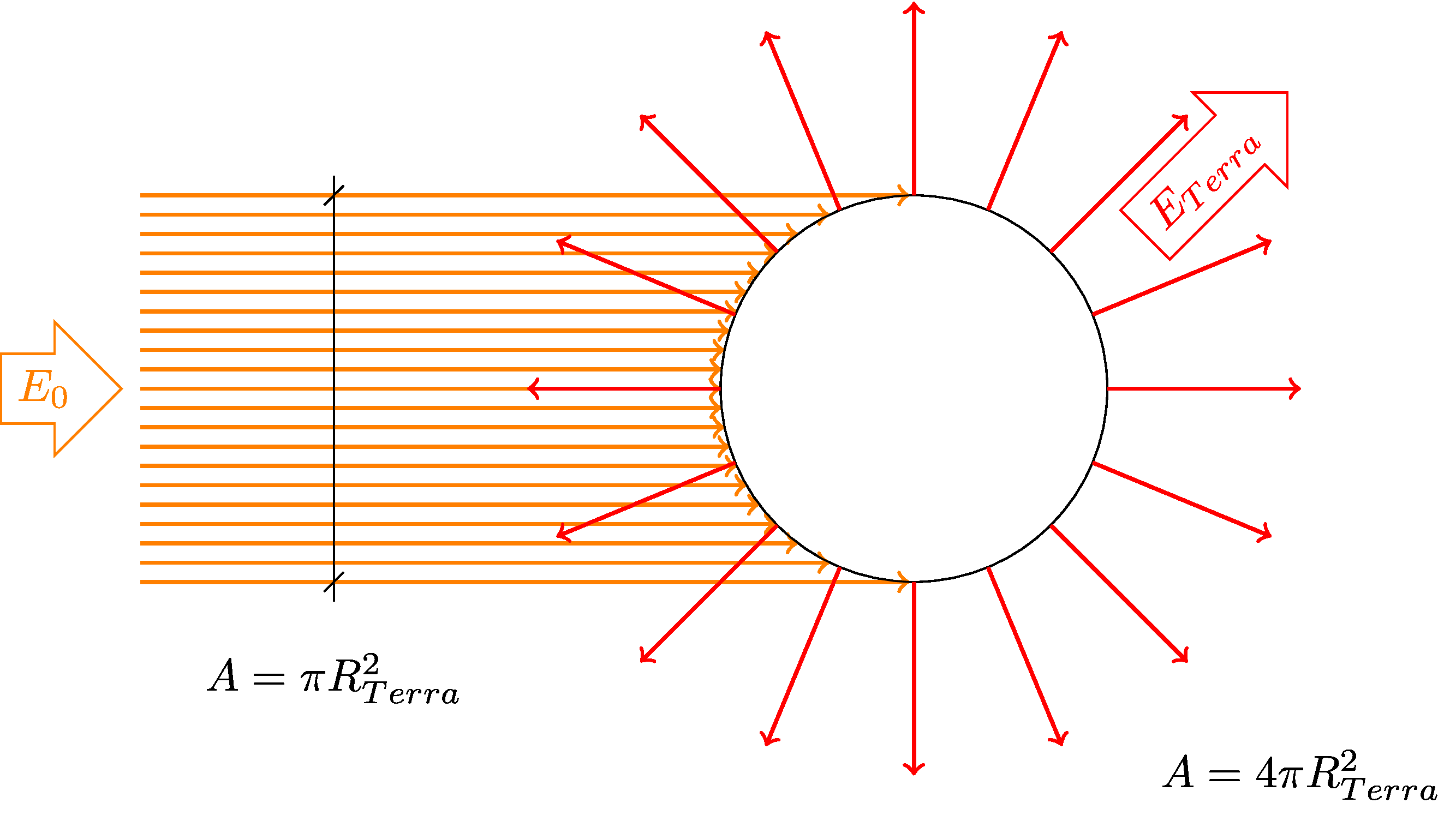
Resolução dos exercícios - 3

• Energia que entra atinge o CÍRCULO de área \(A=\pi R_{terra}^2\).
• Energia que sai, irradia de uma ESFERA de área \(A=4\pi R_{terra}^2\).
• Logo: \[ \phi_{entra} = \phi_{sai} \] \[ E_{entra}A_{disco} = E_{sai} A_{esfera} \] \[ E_0\pi R_t^2 = \sigma T^4 4\pi R_t^2 \] \[ T^4 = \frac{E_0}{4\sigma} = 279K = 6C\].

Resolução dos exercícios - Jupiter

• Dados:
  • Distância orbital: 5,2 UA.
  • Raio 71300km
  • Temperatura: 6000K
• Qual a energia/m2 que atingiria a Terra?
  • Menor distância: \(d_j=4,2\)UA.
  • \(E_J = \sigma T^4 = 7.348\times 10^7\mathrm{W/m^2}\).
  • Fluxo total: \(\phi_J=E_J A_J\).
  • Atinge a terra a irradiância \(E_T = \frac{\phi_J}{4\pi d_J^2}\).
  • Fazendo a conta: \(E_J=3.95\mathrm{W/m^2}\).

Tamanho Aparente do Sol no Céu.

• Tamanho aparente = ângulo no céu.
• Duas maneiras de calcular (simples e menos simples)
• 1a. Geometria simples 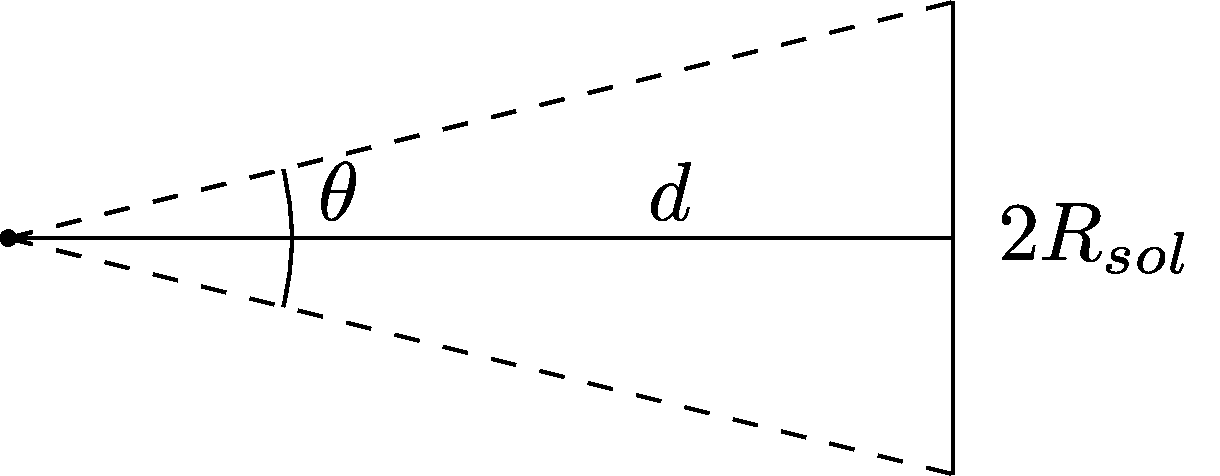\[\tan{(\theta/2)} = \frac{R_{sol}}{d} \qquad \rightarrow \frac{\theta}{2}\approx \frac{R_{sol}}{d}.\]
• Usando os valores: \(R_{sol} = 696340\)km, \(d=1.496\times 10^8\)km, temos: \[ \theta = 0.00931 rad = 0.533^\circ.\]

Tamanho Aparente do Sol no Céu.

• 2a. Usando ângulo sólido
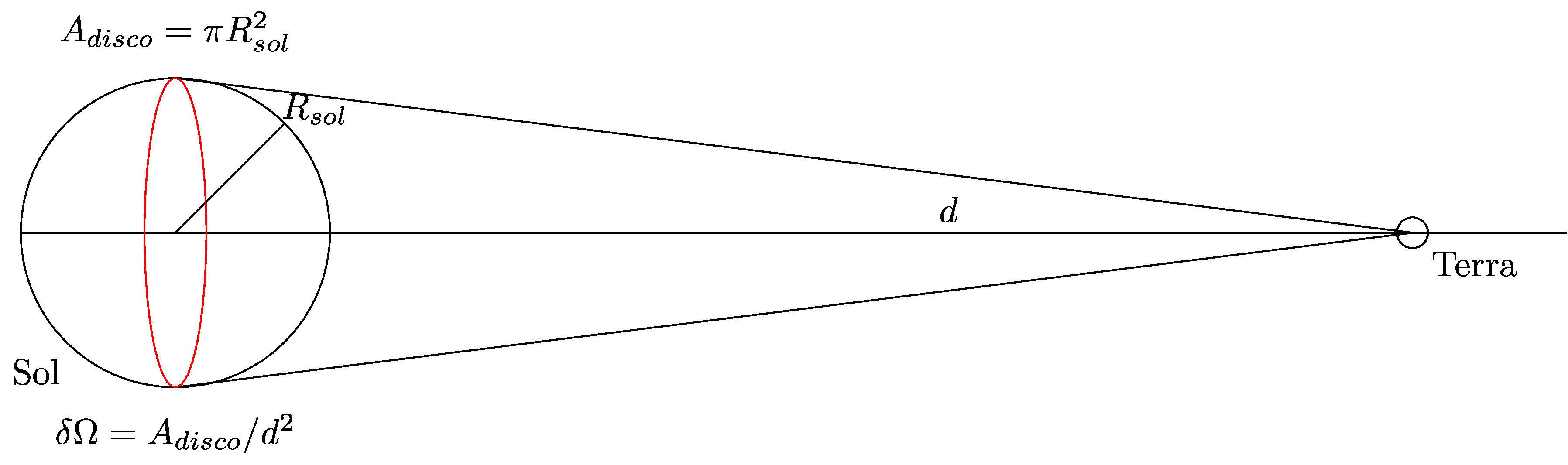
• Onde temos que \(\delta \Omega = 6.807\times 10^{-5}\).
• Imaginando o ângulo sólido \(\delta \Omega\) como um círculo, seu raio seria: 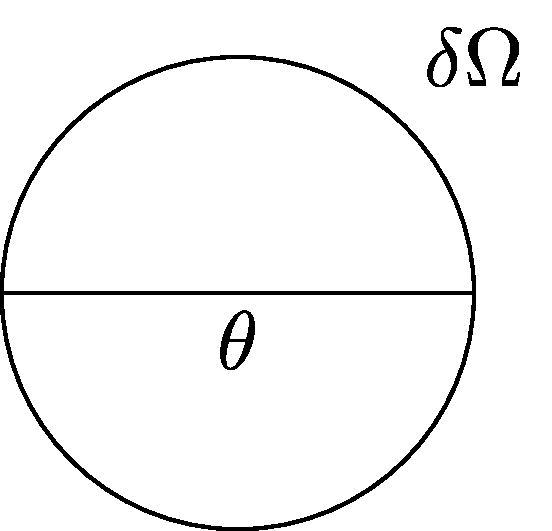\[ \pi \theta^2/4 = \delta \Omega \rightarrow \theta = \sqrt{(4\delta\Omega/\pi)} = 0.00931rad = 0.533^\circ.\]

Sistemas de Coordenadas

• Para localizarmos objetos no céu precisamod de Sistemas de Coordenadas.
• Aqui veremos três tipos:
  • Sistema geográfico.
  • sistema Equatorial Horário.
  • Sistema Horizontal Local.
• Todos consideram uma esfera imaginária no céu, sobre a Terra.
• A trajetória aparente que o Sol executa no céu chama-se “Eclíptica”.

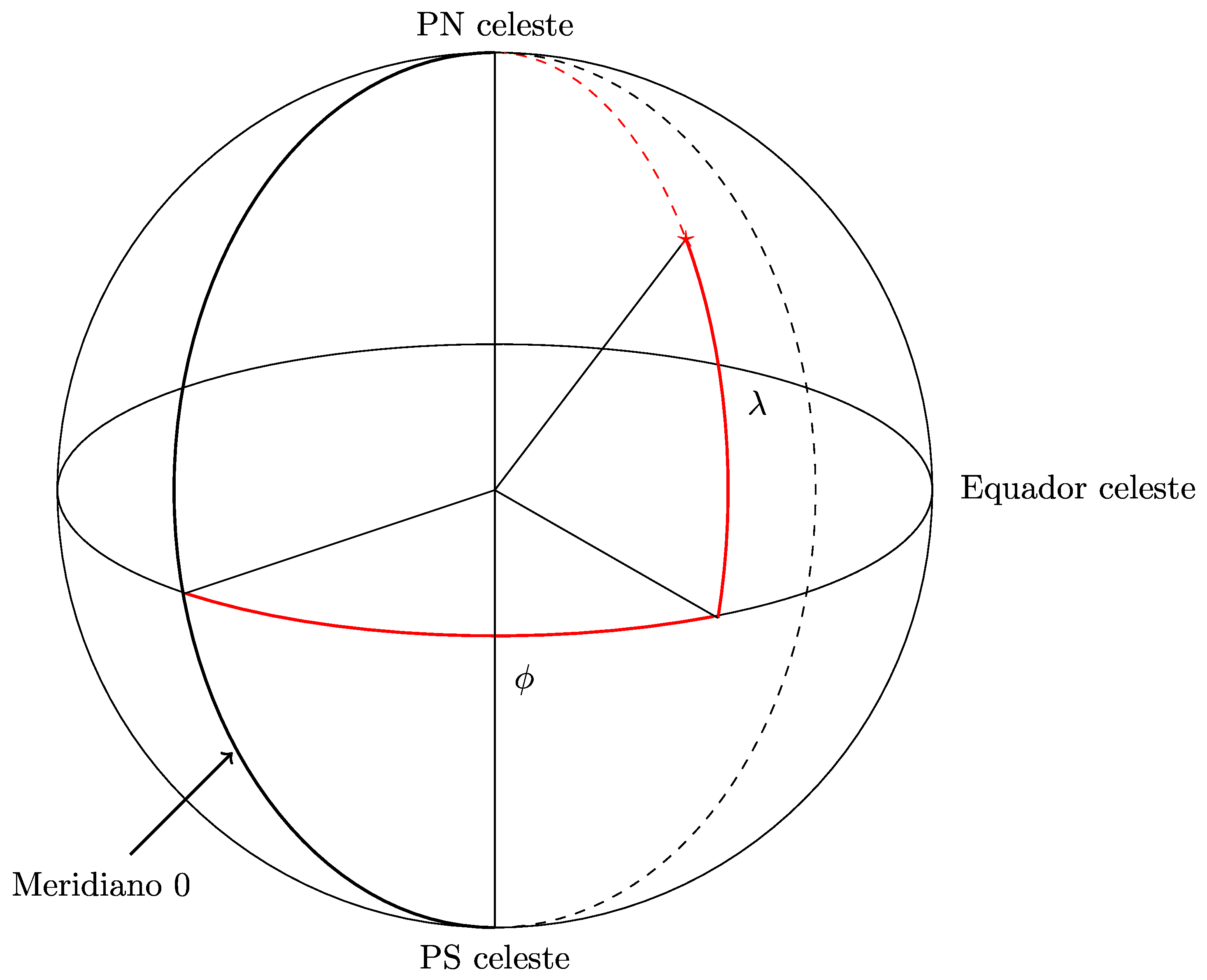
Sistema Geográfico

• A Terra é considerada estática.
• Coordenadas são Latitude (\(\phi\)) e Longitudes (\(\lambda\)) usuais.

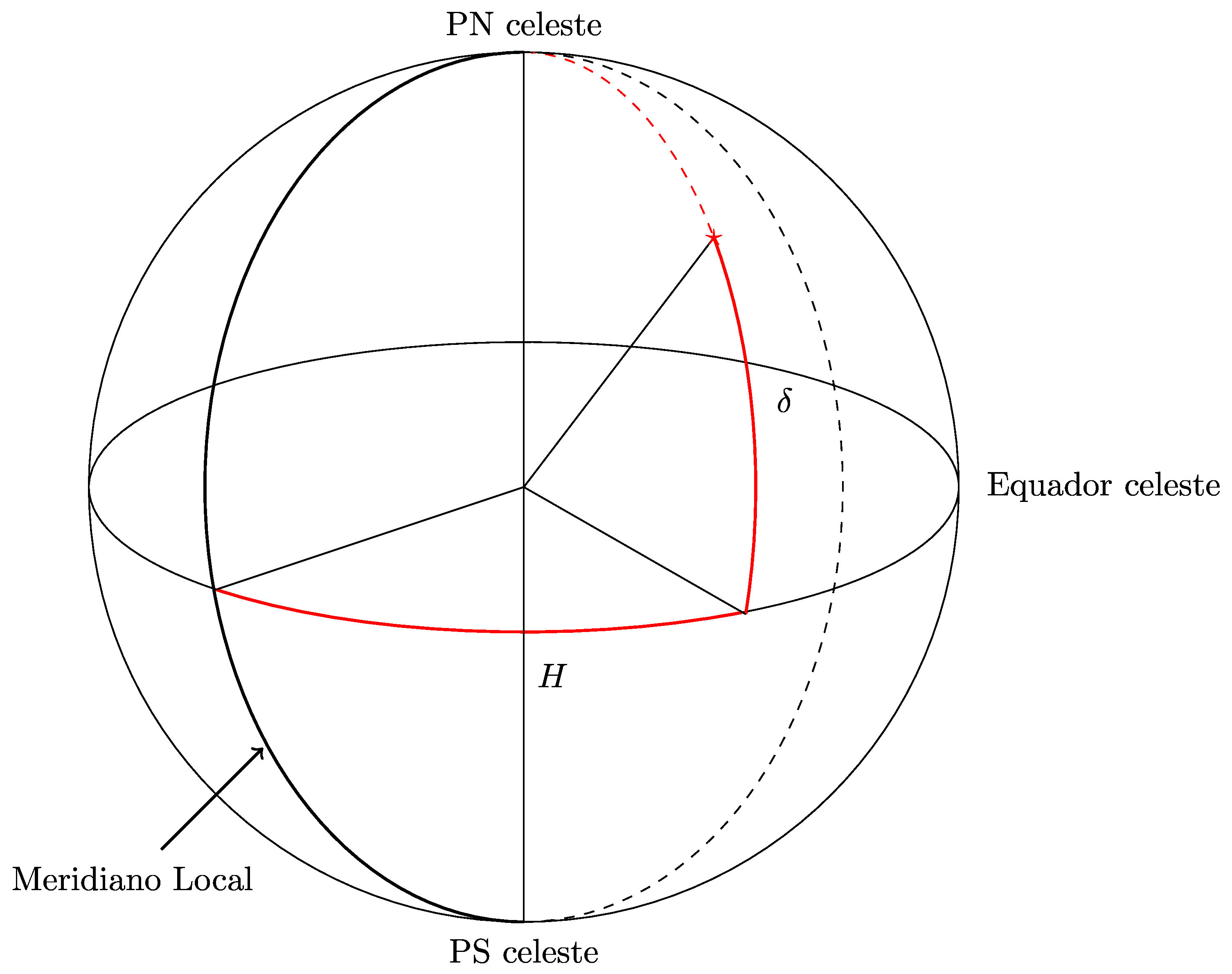
Sistema Equatorial Horário

• É um sistema local, ou seja, as medidas são com relação a posição do observador.
• O Ângulo Horário (\(H\)) é a distância angular do meridiano local até a posição do astro.
  • Note: Um objeto sobre o meridiano local estará exatamente na posição vertical sobre o observador (meio-dia solar).
• \(H\) é medido sobre o Equador Celeste.
  • \(H\) pode ser medido em graus ou em horas (1h=15\({}^\circ\)).
  • \(H<0\) de manhã (a leste do meio-dia solar).
  • \(H>0\) a tarde (a oeste do meio-dia solar).
• A segunda coordenada é a “Declinação” (\(\delta\)), e é uma longitude, contada a partir do equador celeste.
  • \(\delta\) varia entre -90 e 90 graus.

Sistema Equatorial Horário

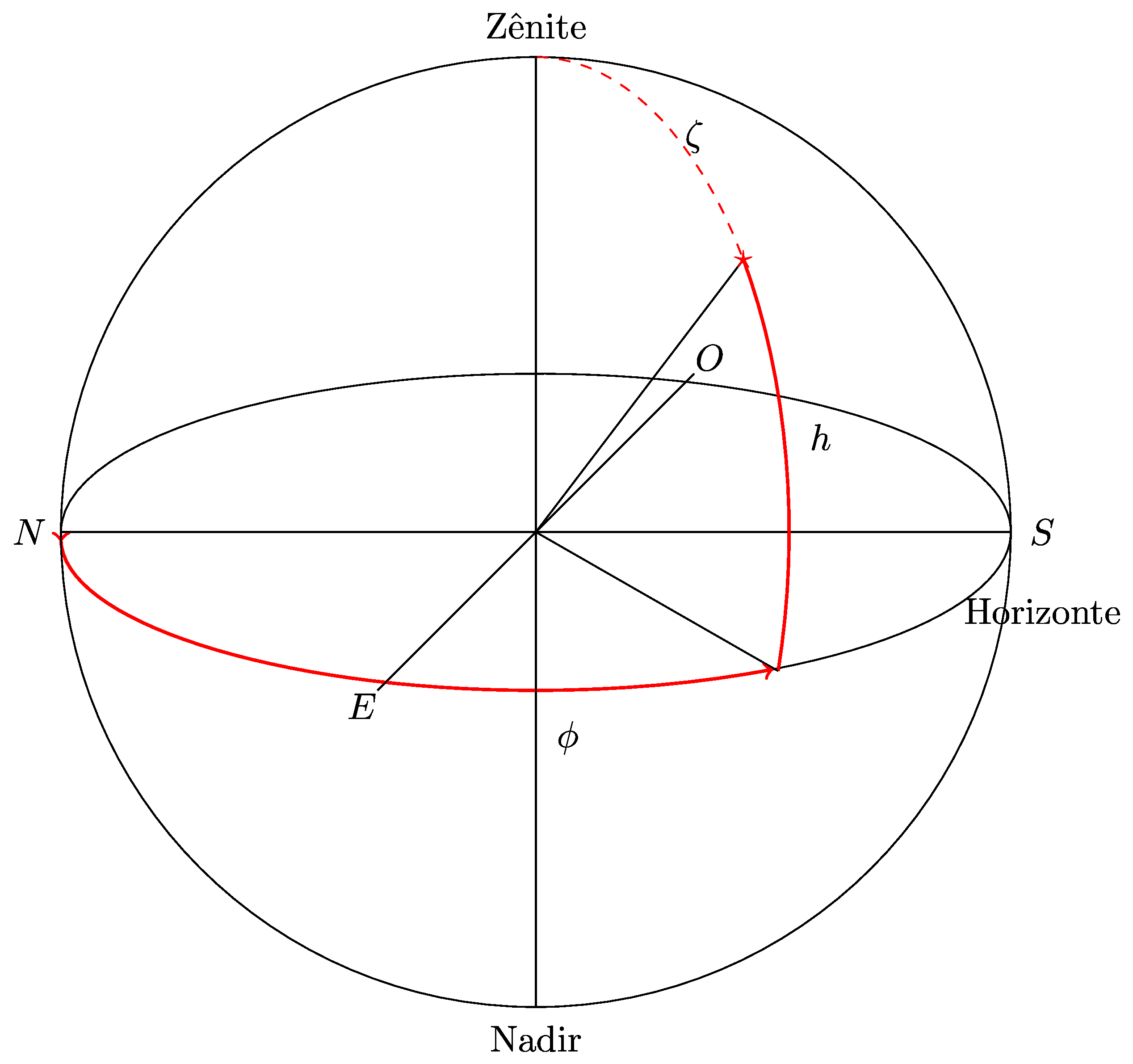
Sistema Horizontal Local

• Este é um sistema local.
• O Zênite é o ponto na esfera celeste imediatamente a cima, na vertical do observador.
  • O oposto do zênite é o nadir, o ponto imediatamente a baixo.
• O plano horizontal (o horizonte) define a parte visível da abóbada celeste, com zênice bem no seu centro.
• O Azimute (\(\phi\)) é a distância angular, na horizontal, entre a direção Norte e a direção do astro.
  • Indo de Norte para Leste. O Azimute varian entre 0 e 360 graus.
• A Elevação (\(h\)) é a distância angular, na vertical, entre o horizonte e a posição do astro.
  • A Distância Azimutal (\(\zeta\)) é o complemento da elevação: a distância angular entre o zênite e o astro, descendo nesses meridianos.

Sistema Horizontal Local