Radiação na Atmosfera
- Prof. Breno Imbiriba
- Periodo especial da PANDEMIA - 2021
- Capítulo 4 - Medição de Irradiância - 2021
Online Math:
https://www.mathcha.io/editor
Radiação de Ondas Curtas
- Radiação Solar - 0,3\(\mu\)m a 4,0\(\mu\)m.
- Devido à emissão de corpo negro do Sol (T=5700K).
- Direta Solar (\(E_s\))
- Raio direto do Sol
- depende só do \(\cos(\zeta)\) e de constituentes atmosféricos
- Difusa (\(E_d\))
- Vinda de TODO O CÉU
- Espalhamento por gases, partículas, núvens...
- Reflexão.
- Irradiância global \(E_g\) é: \[ E_g = E_s + E_d\]
Lei de Beer
- Depende da "Transmitância" da atmosfera: \[E_s = E_0 t_d,\] \(t_d\) é a transmitância direta (fração do feixe incidente que não é absorvido ou espalhado).
- Modelada pela "Lei de Beer":
- para um comprimento de onda \(\lambda\), \[t_d(\lambda) = e^{-\tau(\lambda)/\cos(\zeta_0)},\] onde \(\tau(\lambda)\) é a "profundidade óptica" da atmosfera.
Lei de Beer
Em geral, imagine um tubo cheio de um gás. A transmitância e a profundidade óptica se relacionam (lei de Beer): \[ t_d(\lambda) = e^{-\tau(\lambda)}.\] \[
\begin{array}{ll}
\tau & t_d \\\hline
0 & e^{-0}=1 \\
1 & e^{-1}=37\% \\
2 & e^{-2}=14\% \\
3 & e^{-3}=5\%\\
4 & e^{-4}=1,8\%\\
5 & e^{-5}=0,67\%\\
\infty & e^{-\infty}=0\\
\end{array}
\]
A profundidade óptica \(\tau\) da atmosfera: Medida do solo até o "topo da atmosfera", na vertical (um tubo de 100km...).
Lei de Beer
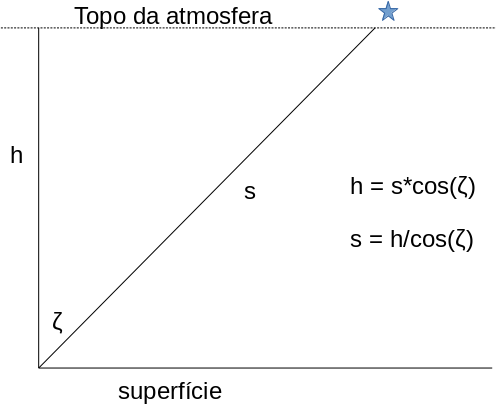
- Quando o objeto não está no zenite, temos que calcular o caminho real da luz:
Lei de Beer
- Logo, o comprimento aumenta de \(1/\cos(\zeta)\), e logo a profundidade óptica também aumenta com o mesmo fator: \[\tau = \tau_0/\cos(\zeta),\] e então \[t = e^{-\tau_0/\cos(\zeta)}.\]
Exercício 4.1
Um balão meteorológico está localizado a 8km de altitude, onde a profundidade óptica relativa ao topo da atmosfera vale 0,03. Um sensor nesse balão mede a radiância monocromática de comprimento de onda \(\lambda\), perpendicular ao sensor, de \(2,0\mathrm{W/m^2/sr/\mu m}\). Na superfície, um fotômetro acaba de medir a profundidade óptica total da atmosfera (para o mesmo comprimento de onda) com valor 0,19. Determinar a radiância espectral: 1. Indicente no topo da atmosfera. 2. Na superfície.
Exercício 4.1 - resolução
À 8km de altitude: \(h=8km, \tau=0.03\), e nessa altitude mede-se (fotômetro): \(R_{8km} =2.0 \mathrm{W/m²/sr/\mu m}\).
Na superfície: \(h=0\), \(\tau =0.19\).
Qual é o valor de \(R\) no topo da atmosfera (\(h=\infty\)), e na superfície (\(h=0\))?.
Lei de Beer: \(t=e^{-\tau }\).
Então: \[
\begin{array}{l}
R_{8km}=R_{0} t_{8km}\\
R_{0km}=R_{0} t_{0km},
\end{array}\]
logo: \[
\begin{array}{lll}
2.0&=&R_{0} e^{-\tau _{8km}} = R_{0} e^{-0.03} \rightarrow R_{0} =2.0/e^{-0.03} = 2.06\mathrm{W/m²/sr/\mu m}\\
R_{0km}&=&R_{0} e^{-0.19} =2.06e^{-0.19} =1.70\mathrm{W/m²/sr/\mu m}.
\end{array}\]
Exercício 4.2
A radiância espectral de \(875\mathrm{W/m^2/sr/\mu m}\) foi medida com um fotômetro solar no instante em que a elevação do Sol era de 35°. A radiância incidente no topo no mesmo comprimento de onda era igual a \(2000\mathrm{W/m^2/sr/\mu m}\). Com base nisso, determinar a profuncidade óptica da atmosfera no instante da medição.
Exercício 4.2 - Resolução
Radiância com sol à 35° = 875W/m²/sr/um. Radiância com o sol a pino = 2000W/m²/sr/um.
Qual é a profundidade óptica da atmosfera neste instante?
\[
E=E_{0} e^{-\tau /\cos \zeta } =E_{0} e^{-\tau \sec \zeta }.
\]
\[
E_{1} =E_{0} e^{-\tau /\cos( 55)}.
\]
\[
E_{2} =E_{0} e^{-\tau /\cos( 0)}.
\]
Então resolve pra \(E_0\) e para \(\tau\).
Radiação de Ondas Longas
- Radiação Terrestre - 4\(\mu\)m a 100\(\mu\)m.
- Devido à emissão de corpo negro da Terra (T=300K).
- Considera-se isotrópica (igual em todas as direções) - A Terra é grande!
- A atmosfera também emite:
- Radiação vem de baixo pra cima (do solo)
- E de Cima pra baix (do Ar)
- Tem que medir ambas as direçõs (dois fotômetros).
Radiação Total e filtros
- A soma das ondas curtas e longas é a "Radiação Total"
- Medidas normalmente são em bandas de comprimento de onda.
- Apontando radiômetros pra cima e pra baixo mede-se diretamente o saldo de radiação.
- Usando um instrumento de ondas longas:
- pode-se mediar a emissividade da superfície.
- Observar certos constituentes atmosféricos gasosos.
- Usando ondas curtas:
- determinação de constituentes atmosféricos como partículas.
- gases que interagem nas onads curtas
- Estudos em impacto ambiental, poluição atmosférica, agrometeorologia, ...
Radiação Total e aplicações
- Medidas podem ser no céu todo - normalmente para cálculos de balanços.
- Podem ser em ângulos sólidos restritos
- Utilizam colimadores
- Medem a radiação de um ponto específico do céu.
- Exemplo: fotômetro solar: Apontam para o Sol e medem a irradiância apenas desta direção (e estimam a profundidade óptica).