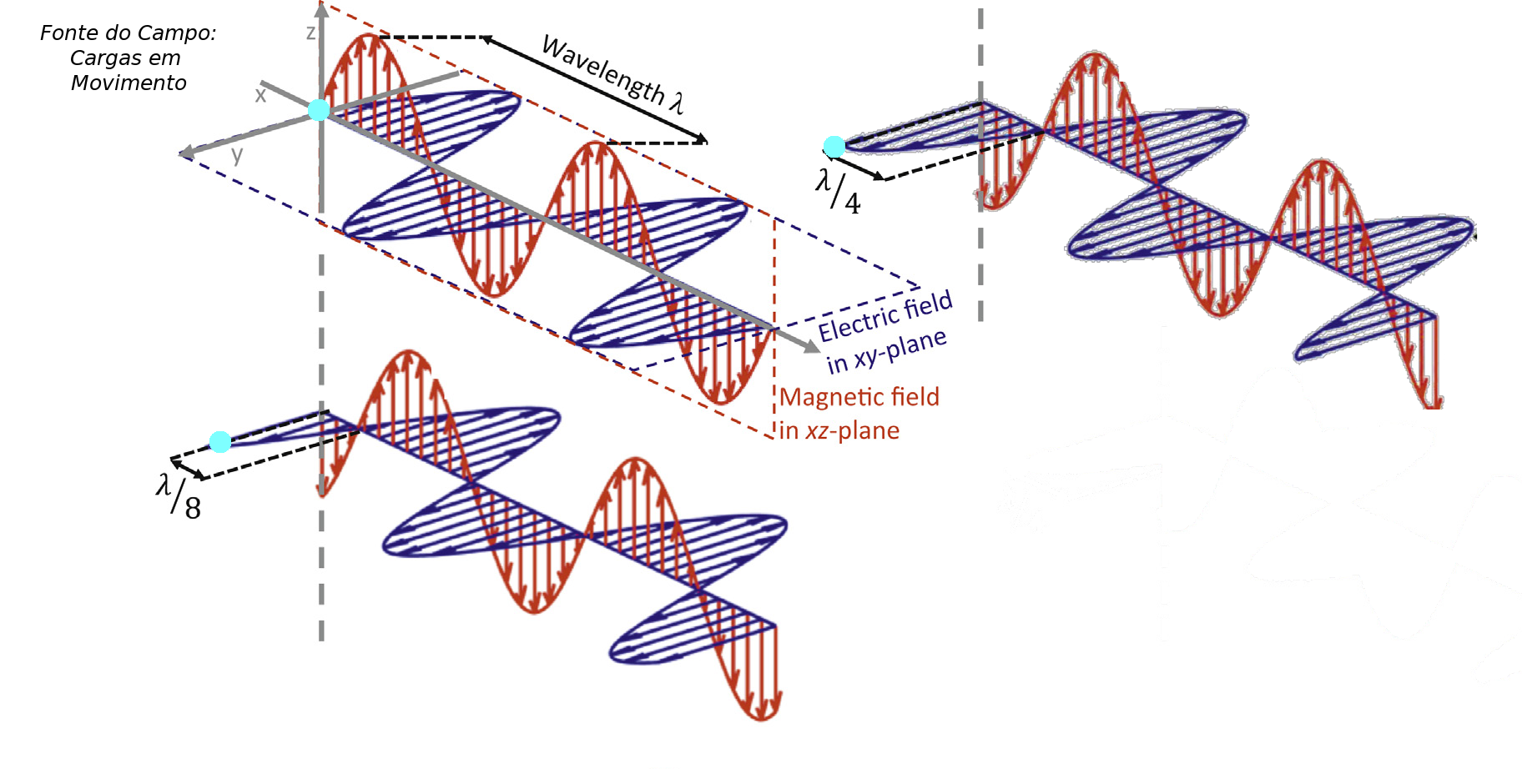

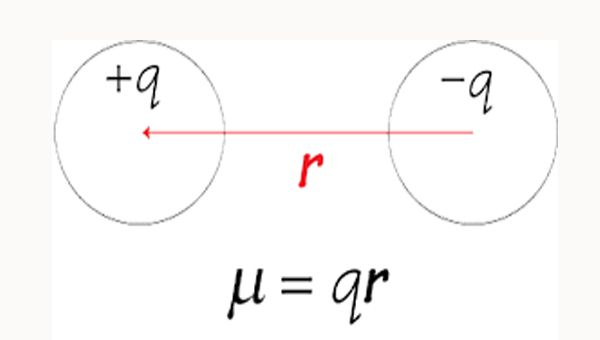
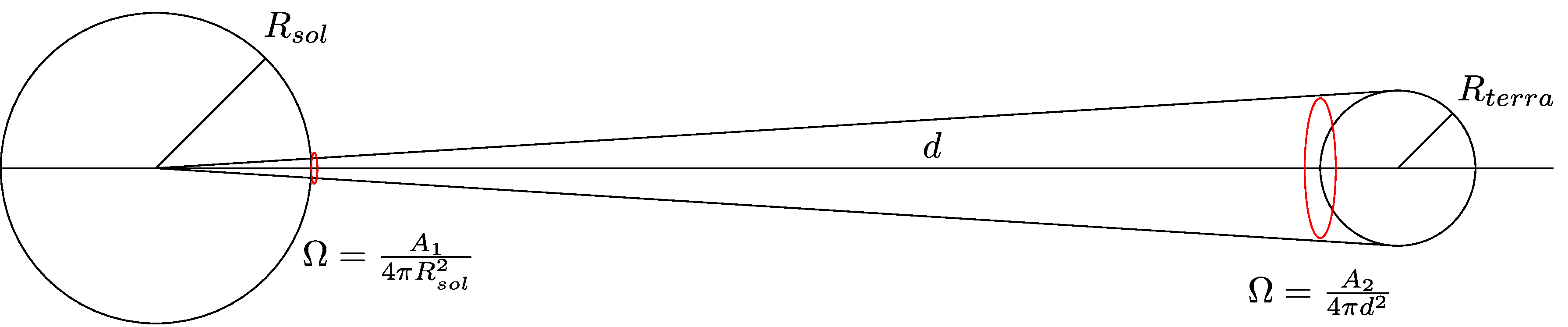
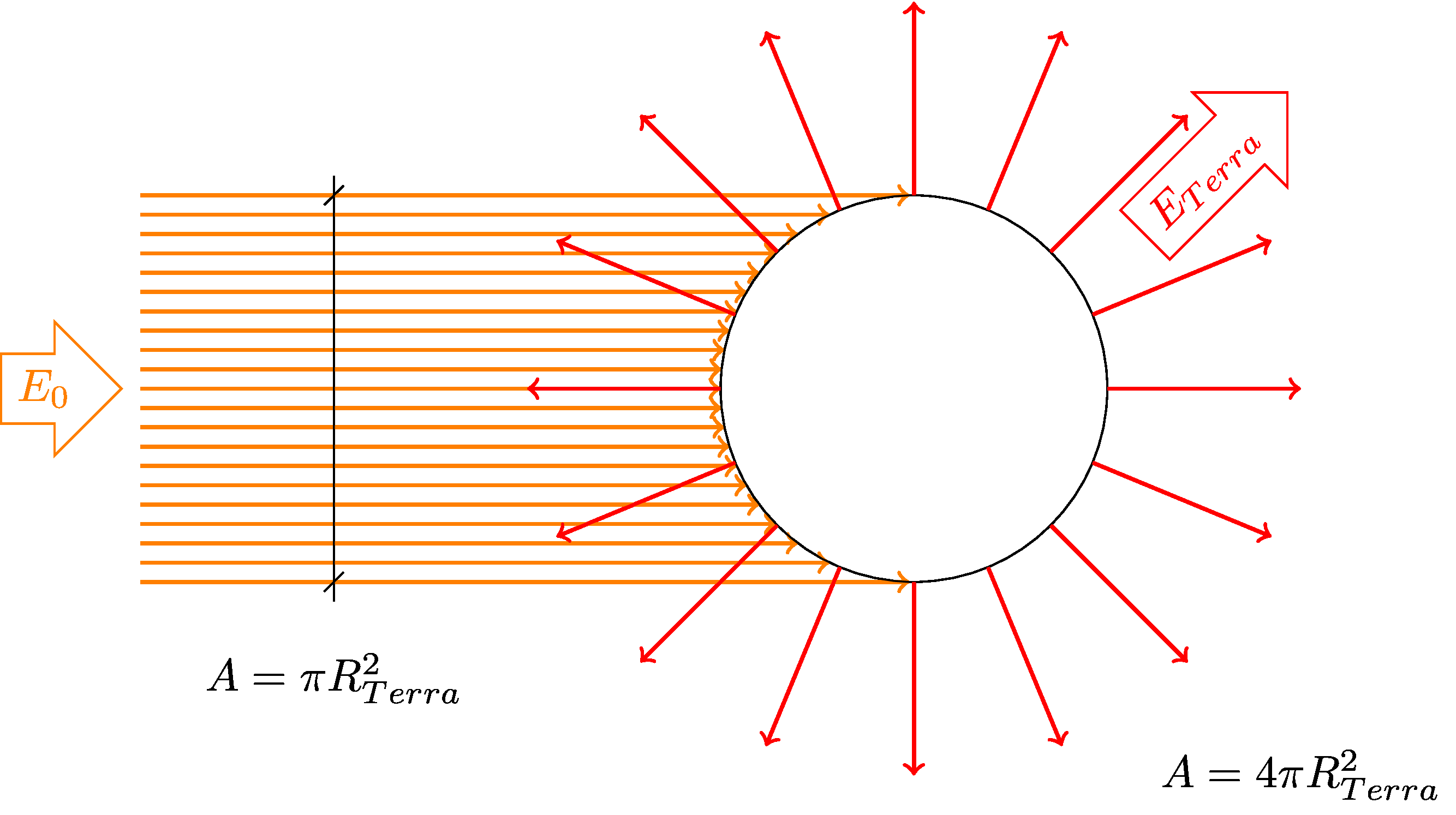

 \[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]
\[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]Onde \(\rho(z)\) é a densidade de massa do gás (g/cm³) no ponto \(z\).
Finalmente, a Profundidade Óptica é: \[\tau_z(\nu) = \int_0^\infty \beta_a(\nu) dz.\]
On usando integrais: \[ I(z) = I_0 e^{-\int_0^z k_a \rho dz}.\]
Note que \(k_a=k_a(p,T)\), e \(\rho=\rho(p,T)\) e por sua vez \(p=p(z)\) e \(T=T(z)\), dependência na altitude \(z\).