

Parametrizado pelo Índide de Refração: 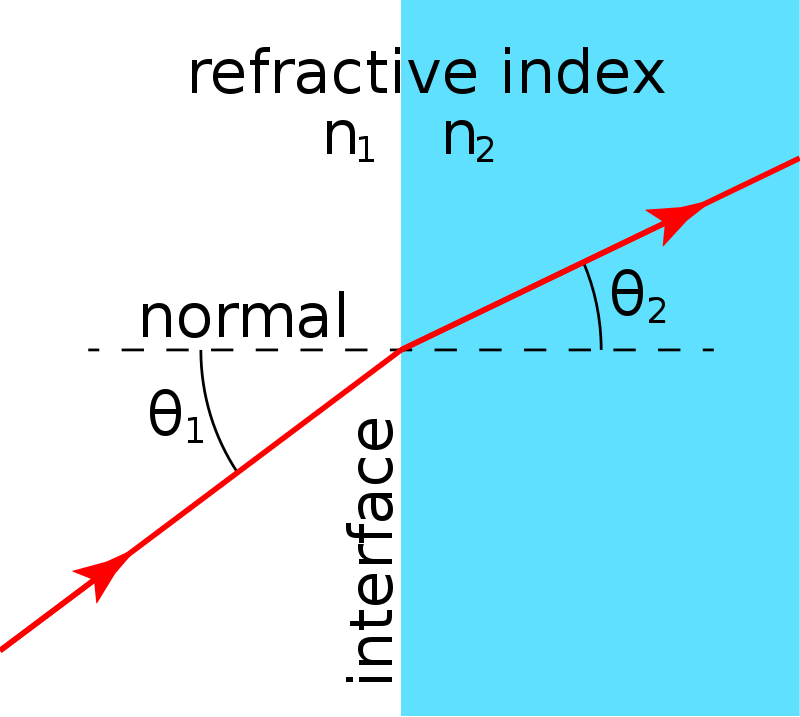
Lei de Snell: \[n_1 \sin\theta1 = n_2\sin\theta2.\]
Ex: \(n_{ar}=1,000293\), \(n_{vidro}=1,52\). Para os dois casos: \(theta_{ar}=0\) e 30 graus, temos: \(\sin\theta_{vidro}=n_{ar}/n_{vidro}\sin\theta_{ar}\). \[\theta_{ar}=0\rightarrow \theta_{vidro}=0.\] \[\theta_{ar}=0\rightarrow \arcsin(1,000293/1,52)\sin30=\arcsin(0,329)=19.21^\circ.\]

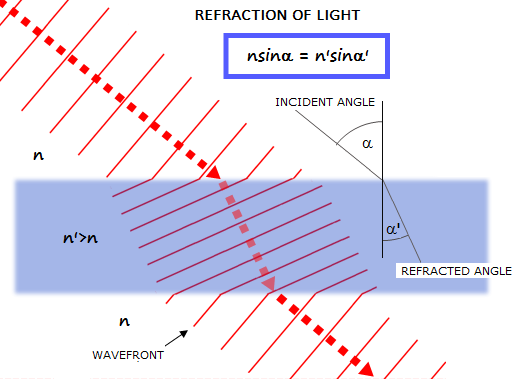
Em uma onda, o índice de refração aje no “número de onda” \(k\): \[ \cos(kx - \nu t)\rightarrow \cos(nkx - \nu t).\]
Como \(v=\lambda \nu = \frac{1}{nk}\nu = \frac{v_0}{n}.\)
O processo de Absorção tembém é descrito usando “índice de refração”, mas esse sendo “complexo”.
Números complexos: \(z=a+bi\), onde \(i=\sqrt{-1}\).
Obedecem a fórmula de Gauss: \[ e^{ia} = \cos{a}+i\sin{a}.\]
Uma onde pode é a parte REAL de uma exponencial imaginária: \[ \cos{(kx-\nu t)} = \Re{e^{i(kx-\nu t)}}. \]
Quando \(n\) é complexo: \(n = n_r + i n_i\) temos: \[ \Re{e^{i((n_r+in_i)kx-\nu t)}} = e^{-2\pi n_i kx}\cos{(kx-\nu t)}.\]
Na verdade, \(n_i\) é diretamente relacionado com o coeficiente de extinção \(\beta\):
Lembrando que a Energia de uma onda é o Quadrado da amplitude, o decaimento exponencial fica: \[ (e^{-2\pi n_i kx})^2 = e^{-\beta x},\qquad \beta=4\pi n_ik\]