Equação da Transferência Radiativa

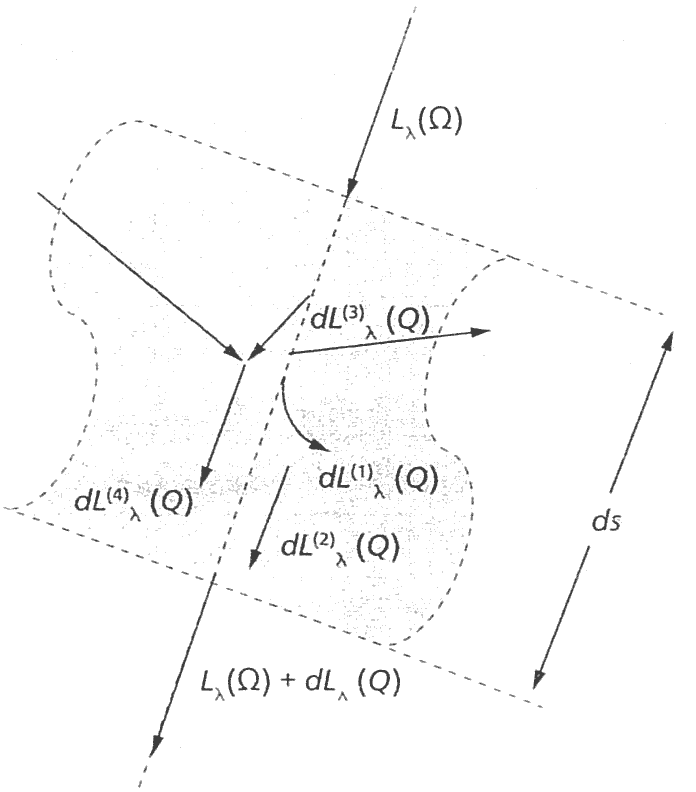
• Quando um feixe \(L_\lambda(\Omega)\) atravessa a matéria pode ocorrer:
  1. Absorção - menos fótons no feixe-> Lei de Beer. (meio molecular absorve energia radiante - aumento da energia interna do meio)
  2. Emissão - mais fótons no feixe. (meio molecular emite energia rafiante - diminuição da energia interna do meio)
  3. Espalhamento de dentro de \(L\) para fora - menos fótons no feixe. (partículas espalham energia radiante para fora do feixe - maior energia para o meio)
  4. Espalhamento de fora de \(L\) para dentro - mais fótons no feixe. (partículas espalham energia de fora do feixe para dentro do feixe - aumento da energia interna do meio).
• Assim: \(dL = -dL^1 + dL^2 - dL^3 + dL^4\):
  • Quando \(dL<0\) energia fica dentro do meio - esquenta!
  • Quando \(dL>0\) energia sai do meio - esfria!

Equação da Transferência Radiativa

ETR com apenas emissão/absorção (sem espalhamento)

• Meio material onde há apenas absorção e emissão eletrônicas/moleculares.
• Sem nenhum espalhamento (sem partículas de tamanho considerável, ignora-se Rayleigh).
• Assim:

\[dL = -dL^{abs} + dL^{emis}.\]

• Já vimos o que é \(dL^{abs}\): \[ dL^{abs}(s) = L(s)\beta_{abs}(s) ds.\]

ETR com apenas emissão/absorção - emis

• O que seria a emissão \(dL^{emis}\)? Lei de Kirchoff:
  • Para um corpo-negro: A Emissividade é igual ao coeficiente de absorção: \[\epsilon_\lambda = a_\lambda = \frac{dL^{abs}{}_\lambda}{L_\lambda} = \beta_{abs}{}_\lambda ds.\]
  • A emissividade é, para corpo-negro de temperatura \(T\) (lei de Plank): \[\epsilon_\lambda = \frac{dL^{emis}{}_\lambda}{B(\lambda,T)}.\]
• Assim: \[dL^{emis} = \epsilon_\lambda B(\lambda,T) = \beta_{abs}{}_\lambda B(\lambda,T) ds.\]

ETR com apenas emissão/absorção (sem espalhamento)

• Juntando ambas as contribuições, temos:

\[ dL = \beta_{abs}(-L + B(T)) ds, \] ou \[ dL_\lambda(\Omega,s) = \beta_{abs}{}_\lambda(s)(-L_\lambda(\Omega,s) + B(\lambda,T(s))) ds, \] ou \[ \frac{dL_\lambda(\Omega,s)}{\beta_{abs}{}_\lambda(s) ds)} = -L_\lambda(\Omega,s) + B_\lambda(T(s)).\]

• Essa é a forma diferencial da ETR sem espalhamento e é chamada de
  • Equação de Schwarzschild

ETR com apenas ESPALHAMENTO (sem absorção/emissão)

• Boa aproximação:
  1. Nas regiões espectrais onde não ocorre emissão/absorção (Janelas)
  2. Ex. visível: Regiões entre 0,35\(\mu\)m e 0,40\(\mu\)m.

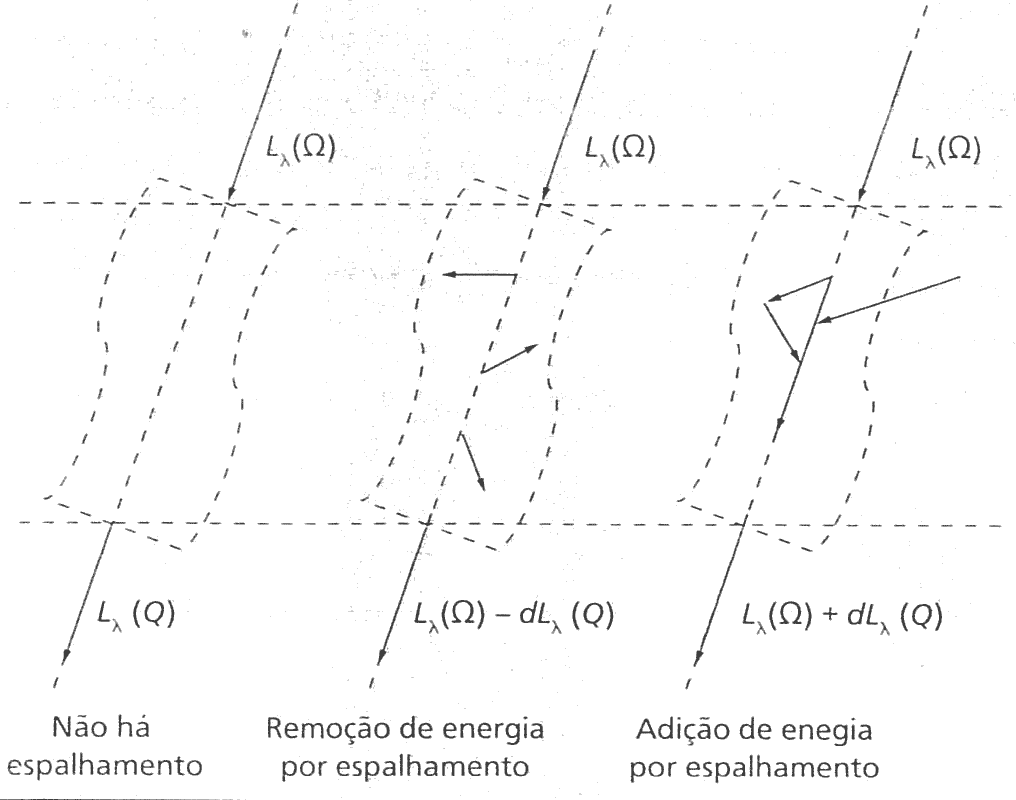
\[ dL = -dL^{fora} + dL^{dentro},\]

• \(dL^{fora}\) - espalhamento da radiação incidente seguindo \(\Omega\) para outras direções.
• \(dL^{dentro}\) - espalhamento de outras direções para a direção de \(\Omega\).
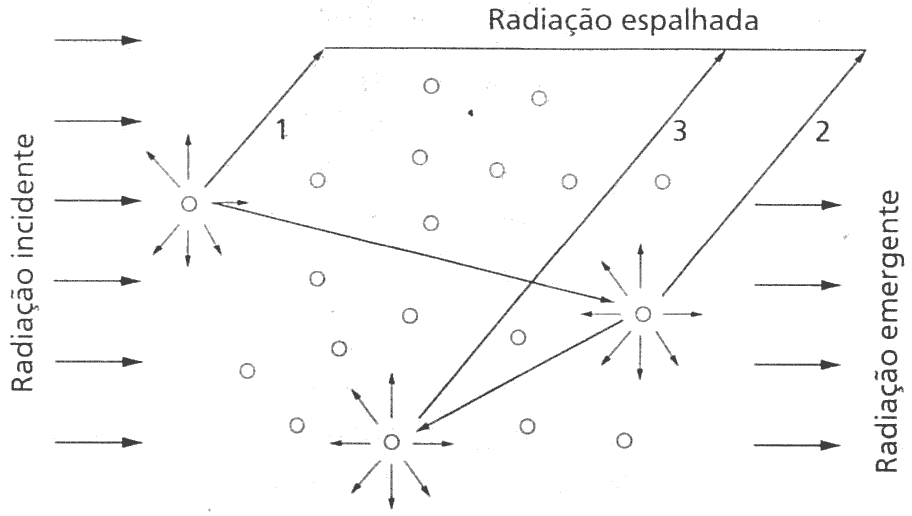
  • O espalhamento pode ser múltiplo: fóton bate em mais de uma partícula.
  • Probabilidade disto aumenta com \(\tau\).

Redução/adição de radiação por espalhamento

Espalhamento múltiplo

ETR com espalhamento

• A atenuação por espalhamento: \[ dL^{fora}(s) = L(s) \beta_{esp}(s)ds.\]

• A adição por espalhamento, vem da radiação difusa (espalhada de outro lugar): \[ dL^{dentro}(\Omega, s) = J(\Omega,s) \beta_{esp}(s)ds.\]

• \(J(\Omega)\) ou \(J_\lambda(\Omega, s)\), é a função fonte por espalhamento:

\[ J(\Omega)=\frac{1}{4\pi}\int_{4\pi}L(\Omega')p(\Omega',\Omega)d\Omega',\] Onde \(L(\Omega')\) é a radiância disponível vindo de outras direções, e \(p(\Omega',\Omega)\) é a função de fase.

Assim: \[ \frac{dL_\lambda(\Omega,s)}{\beta_{esp}{}_\lambda(s)ds} = -L_\lambda(\Omega,s)+J_\lambda(\Omega,s).\]

Equação da Transferência Radiativa - completa

• Juntando todos os quatro fenômenos temos:
  • Todas as variáveis podem depender de \(\lambda\), \(s\) e \(\Omega\):

\[ dL(\Omega) = (-L\beta_{abs} - L\beta_{esp} + B(T)\beta_{abs} + J(\Omega)\beta_{esp}) ds.\]

• Definindo o coeficiente de atenuação total \(\beta=\beta_{abs}+\beta_{esp}\).
• Definindo o Albedo de espalhamento único (single scattering albedo): \(\omega_0 = \beta_{esp}/\beta\), temos que

\[ \beta_{esp}(s) = \omega_0(s)\beta(s),\] \[ \beta_{abs}(s) = (1-\omega_0(s))\beta(s).\]

Equação da Transferência Radiativa - completa

• Trocando na expressão da ETR, temos:

\[ dL = -L\beta ds + B(T(s))(1-\omega_0(s))\beta(s) ds + J(\Omega,s)\omega_0(s)\beta(s) ds,\]

• E assim:

\[ \frac{dL_\lambda(\Omega,s)}{\beta_\lambda(s)ds} = -L_\lambda(\Omega,s) + (1-\omega_0(\lambda,s))B(\lambda,T(s)) + \omega_0(\lambda,s)J(\lambda,\Omega,s).\]