Aproximação de atmosfera plano-paralela (“Terra Plana”)

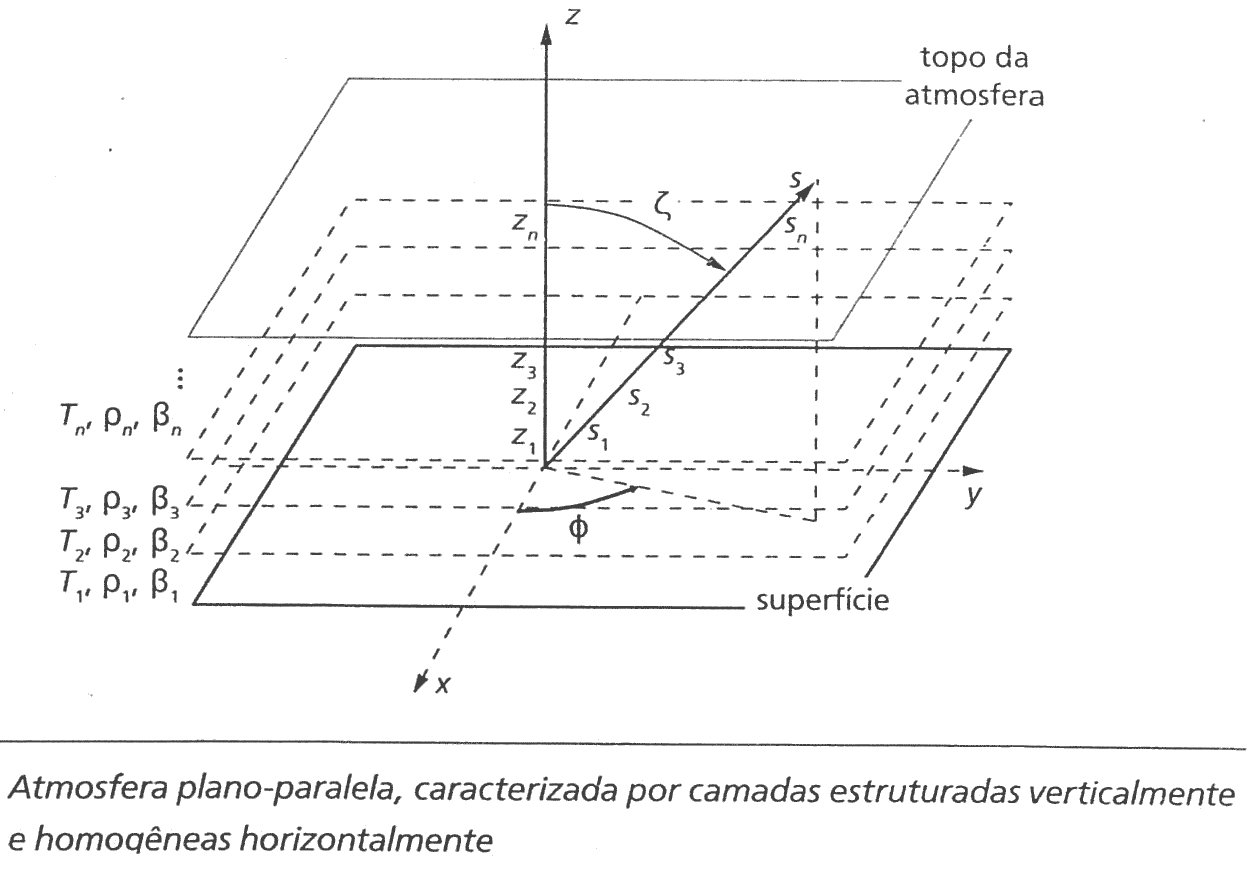
Aproximação de atmosfera plano-paralela (“Terra Plana”)

• Coordenadas Locais: ângulo zenital (\(\zeta\), do topo para baixo) e ângulo azimutal (\(\phi\), do Norte para Leste).
  • Onde define-se: \(\mu=\cos{\zeta}\) (varia de 1 (zenit) ao 0 (horizonte)).
  • Positivo (+) ascendente.
  • Negativo (-) descendente.
• Coordenada do caminho óptico é a própria vertical \(z\) - tudo é função de \(z\).
  • \(z\) é zero no nível do mar,
  • Relação entre \(z\) e o caminho óptico: \(z=s\cos\zeta\) ou \(z=\mu s\).
• A atmosfera é homogênea (constante) na horizontal (\(x\),\(y\)), logo uma grandeza é a mesma estndo exatamente sobre as nossa cabeças ou em um outro ângulo, o que importa é a altitude.

Aproximação de atmosfera plano-paralela (“Terra Plana”)

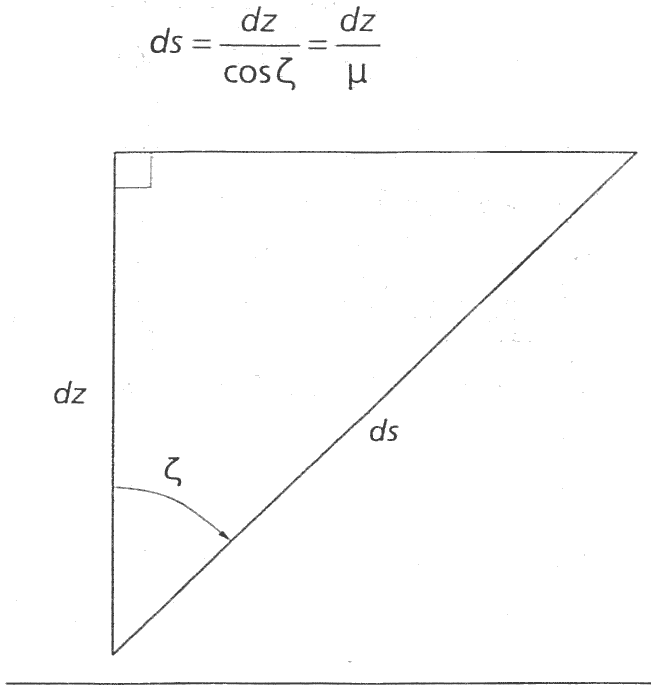
• Como a atmosfera muda com \(z\), há a relação entre \(ds\) e \(dz\):

Integral da ETR na atmosfera Plano-Paralela

\[ \frac{dL_\lambda(\Omega,s)}{\beta_\lambda(s)ds} = -L_\lambda(\Omega,s) + (1-\omega_0(\lambda,s))B(\lambda,T(s)) + \omega_0(\lambda,s)J(\lambda,\Omega,s).\]

1. Vamos trocar o “abstrato” \(\Omega\) pelos “concretos” \(\zeta\) e \(\phi\).
2. A profundidade óptica é dada por \(\frac{d\tau(z)}{dz}=-\beta(z)\).
3. O efeito do ângulo de visada \(\zeta\) entra na definição de \(ds\), assim temos:

\[ \frac{\mu dL_\lambda(z,\mu,\phi)}{\beta_\lambda(z)dz} = -L_\lambda(z,\mu,\phi) + (1-\omega_0(z))B(T(z)) + \omega_0(z)J(z,\mu,\phi).\]

• Como função de \(\tau\) é uma E.D.O 1a ordem - que tem solução geral.