Balanços Radiativos

• Em qualquer sistema, balanço: \(E^\text{abs} - E^\text{emit} = Q^\text{int}\).
  • \(E\) (ou \(Q\)) aqui é o total de todas as formas de energia.
• No sistema da Terra, e no balanço radiativo normalmente dividimos as energias entre:
  • \(E_c\): Ondas curtas: IR próximo, Vis, UV
  • \(E_l\): Ondas longas: IR Termal
  • Claro que existem outras formas de energia (calores sensíveis, latentes, mecânica, etc… mas não importam neste momento)

Balanços Radiativos

• Assim temos: \[ Q^\text{int} = (E_c{}^{abs}-E_c{}^{emit})+(E_l{}^{abs}-E_l{}^{emit}) = Q_c{}^{tot}+Q_l{}^{tot},\] \[ Q^\text{int} = (E_c{}^{abs}+E_l{}^{abs}) - (E_c{}^{emit}+E_l{}^{emit}) = Q^{abs}-Q{}^{emit}.\]

• No caso de balanço, \(Q^\text{int}=0\rightarrow Q^{abs}=Q^{emit}\). \[ Q_{abs} = Q_{emit} \rightarrow \int_0^\lambda Q_{abs}(\lambda)d\lambda = \int_0^\lambda Q_{emit}(\lambda)d\lambda.\]

Equilíbrio radiativo do Planeta - SEM ATMOSFERA

Equilíbrio radiativo do Planeta - SEM ATMOSFERA

• Superfície do Planeta banhada por radiação de ondas curtas de irradiância \(E_0\) (W/m²): \(A=\pi R^2\).

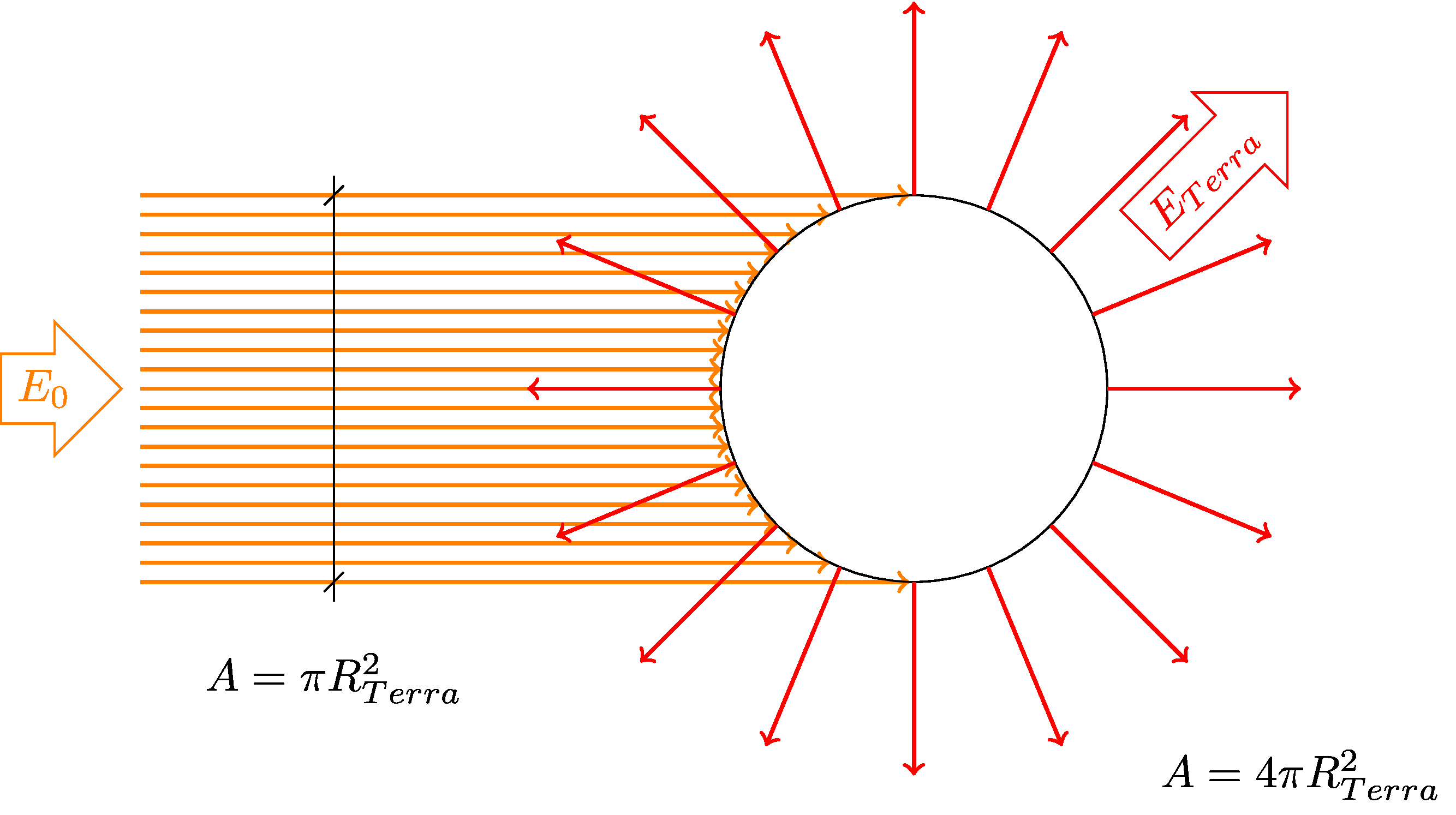
• Albedo planetário \(r_s\) é a quantidade de radiação refletida de volta ao Espaço.

• Emissão pela superfície de todo o Planeta devido à sua temperatura T (lei de Steffan): \(E = \sigma T^4 4\pi R^2\).

Equilíbrio radiativo do Planeta - SEM ATMOSFERA

• Assim: \[ E_0(1-r_s) \pi R^2 = \sigma T^4 4\pi R^2,\] ou \[ T = \left[\frac{(1-r_s)E_0}{4\sigma}\right]^{1/4}.\]

• No caso da Terra:
  • \(E_0=1367\)W/m², \(r_s\approx 0,3\), assim:
  • \(T\approx 255\)K. Gelado! Porque não tem atmosfera….
  • Mesmo se o albedo fosse zero, T=279K, ainda frio.
  • A atmosfera faz toda a diferença.

• Ex. Calcule a temperatura da superfície da Lua.