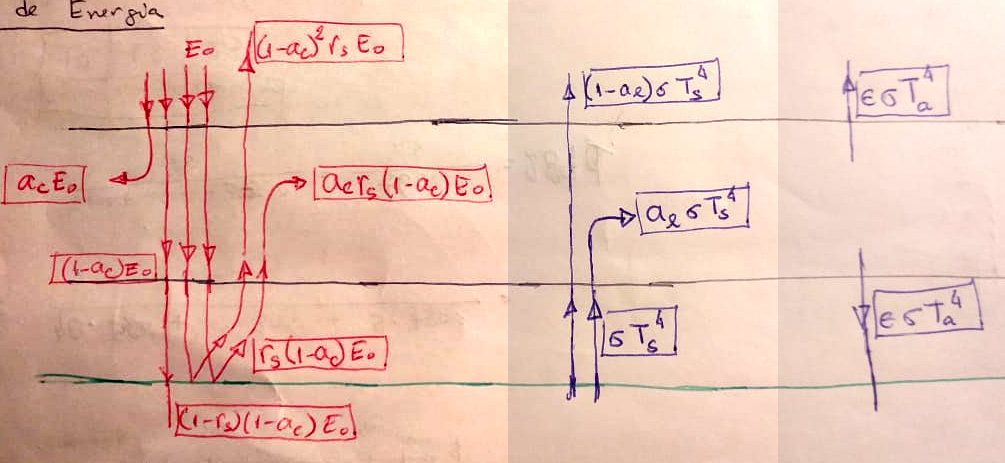

Balanco na Superfície: \[ (1-r_s)(1-a_c) E + a_l\sigma T_a^4 = \sigma T_s^4.\]

Balanco na Atmosfera: \[ a_cE + a_cr_s(1-a_c)E + a_l\sigma T_s^4 = 2a_l \sigma T_a^4.\]

Balanco no Topo da Atmosfera: \[ E = (1-a_c)^2r_sE + (1-a_l)\sigma T_s^4 + a_l\sigma T_a^4. \]

\[ (1-r_s)(1-a_c) E + a_l\sigma T_a^4 = \sigma T_s^4.\] \[ a_cE + a_cr_s(1-a_c)E + a_l\sigma T_s^4 = 2a_l \sigma T_a^4.\] \[ E = (1-a_c)^2r_sE + (1-a_l)\sigma T_s^4 + a_l\sigma T_a^4. \]
As variáveis são \(T_a\) e \(T_s\) logo bastam duas equações (a 1a e a 2a). A 3a equação é automaticamente consistente, na verdade ela é a soma da 1a com a 2a!!
TENTE FAZER!
As equações são (reescrevendo o 1o termo da segunda equação):
\[ (1-r_s)(1-a_c)E + a_l\sigma T_a^4 = \textcolor{red}{\sigma T_s^4}, \]
\[ a_c(1+r_s(1-a_c))E + a_l\textcolor{red}{\sigma T_s^4} = 2 a_l\sigma T_a^4.\]
Substituindo a 1a na 2a equação, temos:
\[ \underbrace{a_c(1+r_s(1-a_c))E + a_l(1-r_s)(1-a_c)E}_{\text{mantem este como está}} + \underbrace{a_l^2\sigma T_a^4 = 2a_l \sigma T_a^4}_{=(2a_l-a^2)\sigma T_a^4 = a_l(2-a_l)\sigma T_a^4}, \]
assim:
\[ T_a^4 = \frac{\left\{ a_c\left(1+r_s(1-a_c)\right)+a_l(1-r_s)(1-a_c)\right\} E}{a_l(1-a_l)\sigma}.\]
E para \(T_s\):
\[ T_s^4 = \frac{1}{\sigma}\left( \textcolor{red}{(1-r_s)(1-a_c)}E + \frac{a_c(1+r_s(1-a_c))+a_l\textcolor{red}{(1-r_s)(1-a_c)}}{2-a_l}E\right) = \] \[ = \frac{\textcolor{green}{(2-a_l)}\textcolor{red}{(1-r_s)(1-a_c)} + a_l\textcolor{red}{(1-r_s)(1-a_c)} + a_c(1+r_s(1-a_c))}{\textcolor{green}{(2-a_l)}\sigma} E = \] \[ = \frac{2(1-r_s)(1-a_c)+a_c(1+r_s(1-a_c))}{(2-a_l)\sigma}E.\]
Este caso é problemático, pois a nossa solução envolve divisões por \(a_l\). SEMPRE que se faz isso, assume-se que \(a_l\) não é zero explicitamente! Ao fazer \(a_l=0\) obtemos \(T_a = 0/0\) o que é uma indeterminação.
Na verdade o sistema de equações montado não contempla esta solução pois a 2a equação ficaria da forma: \[ 0 = 0 \sigma T_a^4, \] ou seja, qualquer valor de \(T_a\) resolve o problema. Uma atmosfera totalmente transparente não troca energias com o meio, logo ela pode ter qualquer temperatura!
Já a temperatura da superfície torna-se: \[ T_s^4 = \frac{1}{\sigma}(1-r_s)(1-a_c)E,\] como obtido no caso anterior do planeta sem atmosfera.
As temperaturas tornam-se:
\[T_a^4 = \frac{a_c + a_l(1-a_c)}{a_l(2-a_l)}\frac{E}{\sigma}, \qquad T_s^4 = \frac{2-a_c}{2-a_l}\frac{E}{\sigma}.\]
As temperaturas apenas dependem de \(E\), do coeficiente de absorpção de ondas curtas e de ondas longas.
\[ T_a = 257K = -15C,\qquad T_s = 288K = 15C.\]
\[ T_a = 277K = 4C,\qquad T_s = 291K = 18C.\] Aqui o efeito estufa está caracterizado pelo aumento do espalhamento atmosférico e pela absorção total das ondas longas.
Considere uma camada atmosférica com:
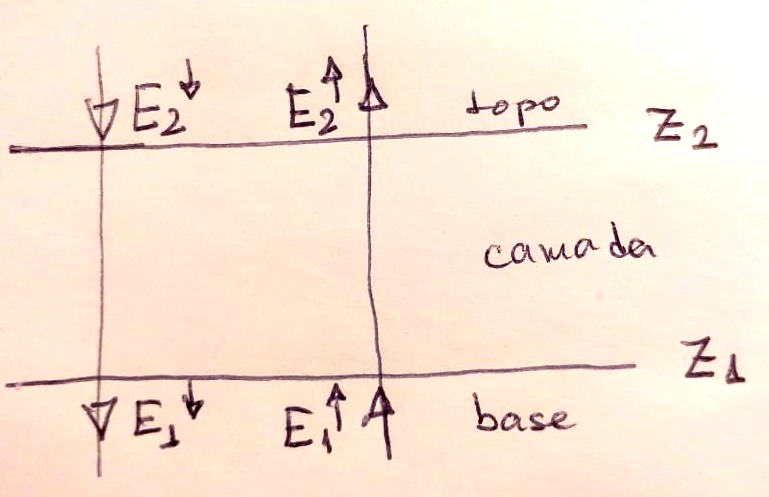

A conservação de energia nessa camada atmosférica é dada por: \[\Delta E = E_\text{entra} - E_\text{sai} = E(z_2)^{\downarrow} + E(z_1)^{\uparrow} - E(z_1)^{\downarrow} - E(z_2)^{\uparrow} = \] \[ = (E(z_2)^{\downarrow} - E(z_1)^{\downarrow}) - (E(z_2)^{\uparrow} - E(z_1)^{\uparrow}) = \] \[ = \Delta E^{\downarrow} - \Delta E^{\uparrow}.\]
No Equilíbrio: \[\Delta E^{\downarrow} = \Delta E^{\uparrow},\] mas quando não estamos no equilíbrio, há mudança da energia interna.
1a. lei da Termodinâmica: \[ \Delta E_\text{int} = \Delta Q + \Delta W.\]
O termo \(\Delta W\) é o trabalho realizado sobre o sistema. Trabalho é \(F.x\), logo tem que haver deslocamento. Se a atmosfera for considerada estático (não aumentar ou diminuir de volume) então \(\Delta W = 0\), logo: \[ \Delta E_\text{int} = \Delta Q.\]
\[ \Delta E_\text{int} = \Delta Q = m c_p \Delta T.\]
A massa é dada por \(m = V\rho = A\Delta z \rho\), onde \(A\) é a área da camada. Dividindo tudo por \(A\), transformamos \(E\) de J para J/m²: \[\Delta E_\text{int} = \Delta z \rho c_p \Delta T.\]
Para termos a variação no tempo e irmos de energia para fluxo de energia, precisamos dividir por um intervalo de tempo \(\Delta t\): \[\Delta I_\text{int} = \Delta z \rho c_p \frac{\Delta T}{\Delta t},\]
\[\Delta I_\text{int} = \Delta z \rho c_p \frac{\Delta T}{\Delta t},\] onde \(I\) é agora em W/m², e é a mudança do fluxo radiante entre o topo e a base da camada. Finalmente, dividindo tudo por \(\Delta z\), temos:
\[ \frac{dI}{dz} = \rho c_p \frac{dT}{dt}.\]
O termo \(\frac{dI}{dz}\) representa o Divergente da radiância: \[\vv{\nabla}\cdot \vv{I} = \rho c_p \frac{dT}{dt},\] e na verdade é igual a equação da propagação do calor.
Na superfície ocorrem trocas de energia tanto radiativas quanto não-radiativas.
Há ainda outras formas de troca de energia, vento, corpos aquáticos, …, mas esses são os básicos.
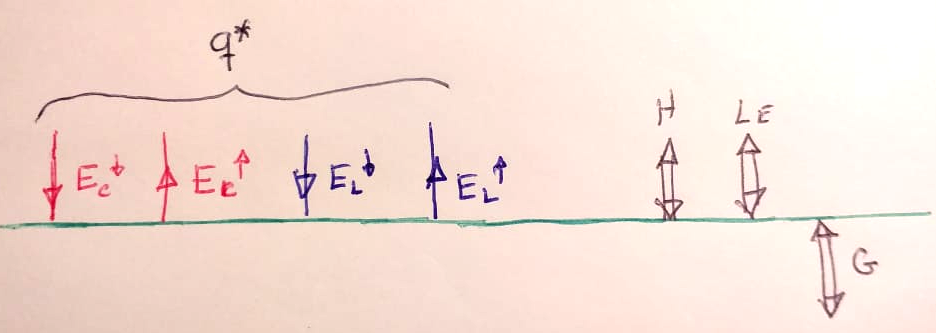
A equação do balanço radiativo fica na forma:
\[ q* = H + L_e + G.\]

As variáveis \(H\), \(L_e\) e \(G\) são derivadas das condições meteorológicas (temperatura, umidade, ventos, etc…) e de propriedades do solo (capacidade térmica da superfície, evapotranspiração, etc…).
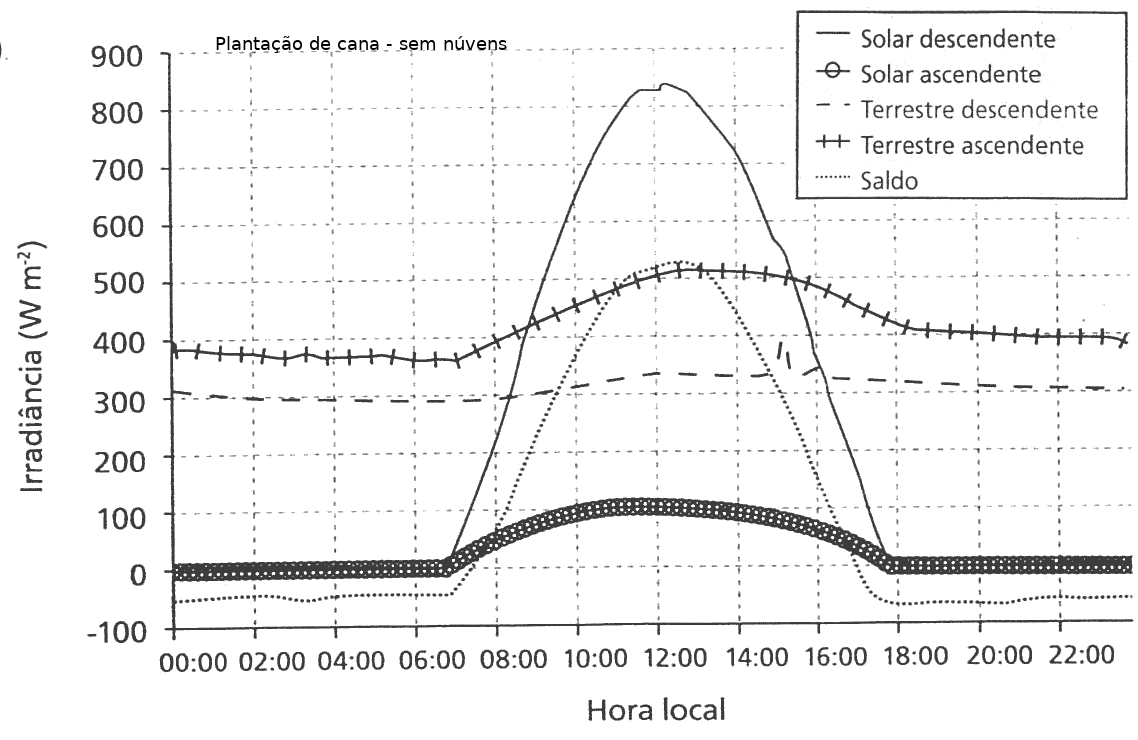
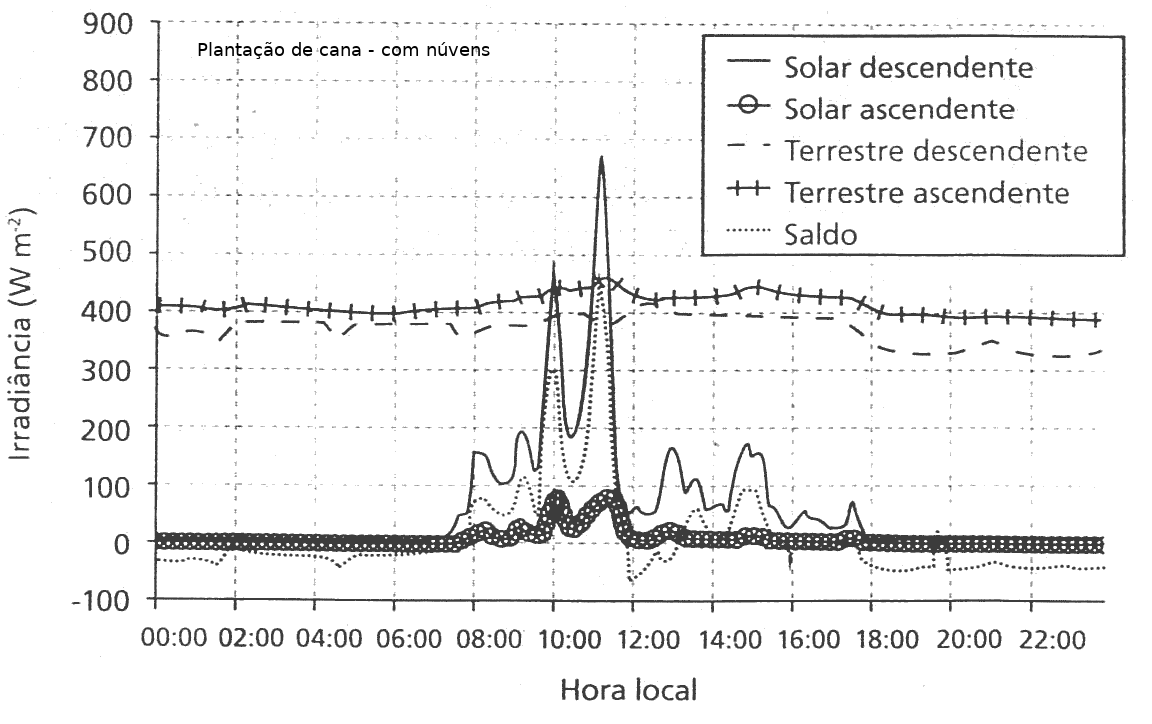
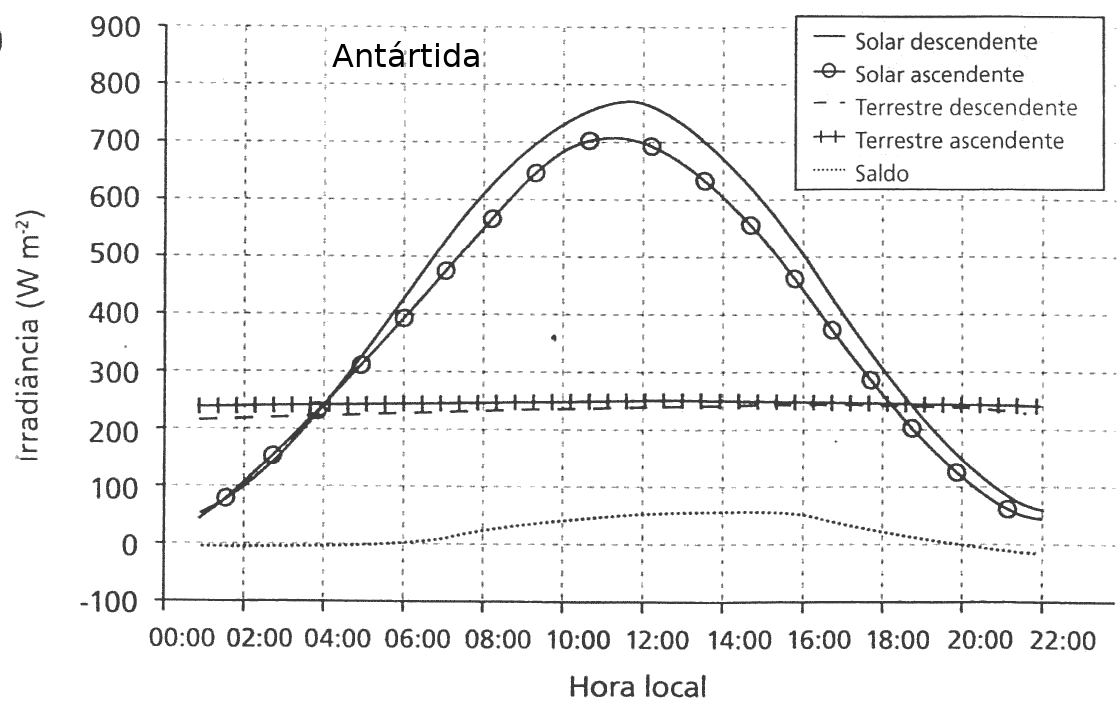
Já o valor do saldo radiativo \(q*\) é normalmente medido empiricamente atraves de radiômetros: