Radiação na Atmosfera
- Prof. Breno Imbiriba
- Periodo especial da PANDEMIA - 2020
- Aula 1 - 9/set/2020
Radiação Eletromagnética
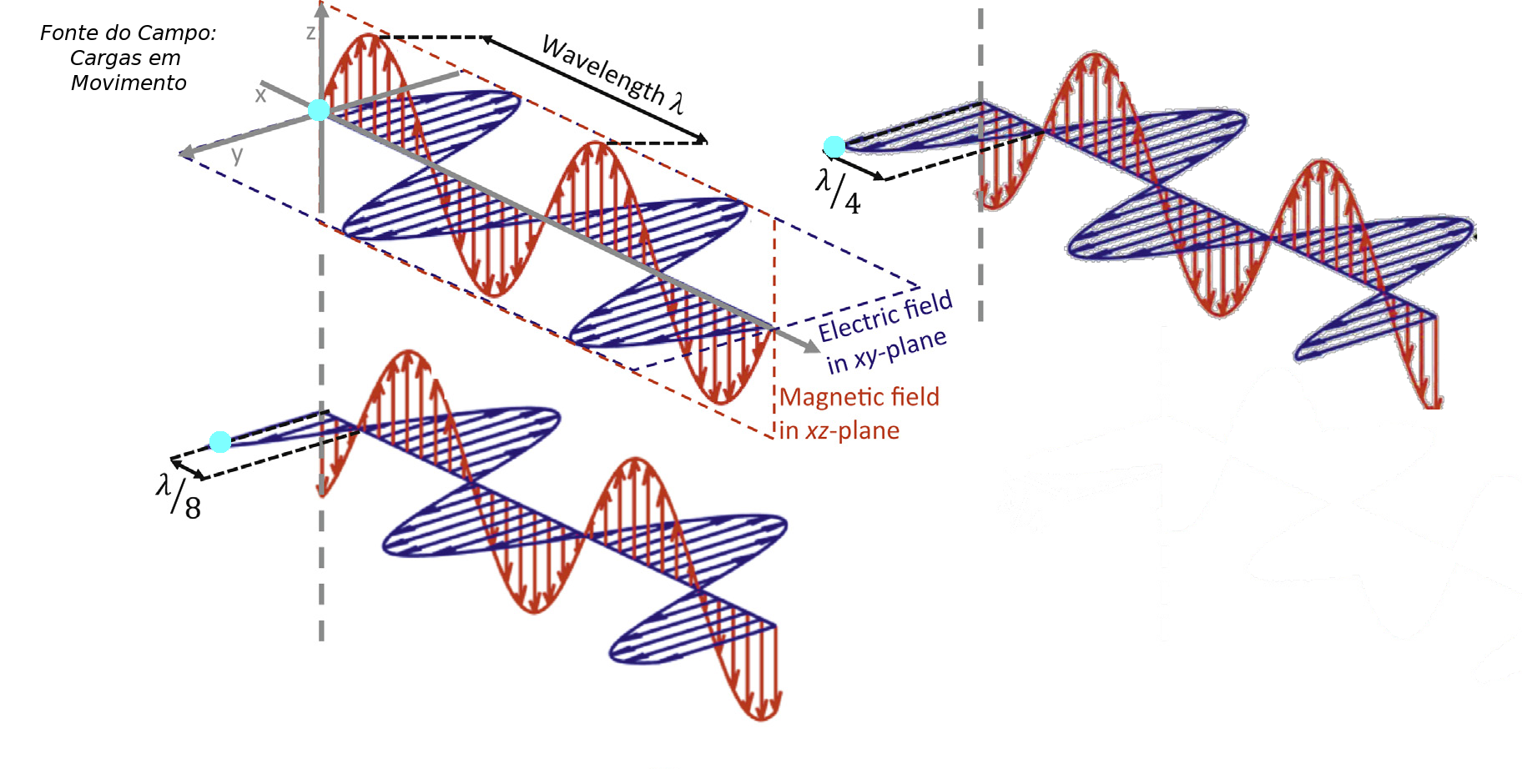
Campos e propagação
- Descoberta por Maxwell - (equações de Maxwell do Eletromagnetísmo)
- Onda formada de campos elétricos e magnéticos.
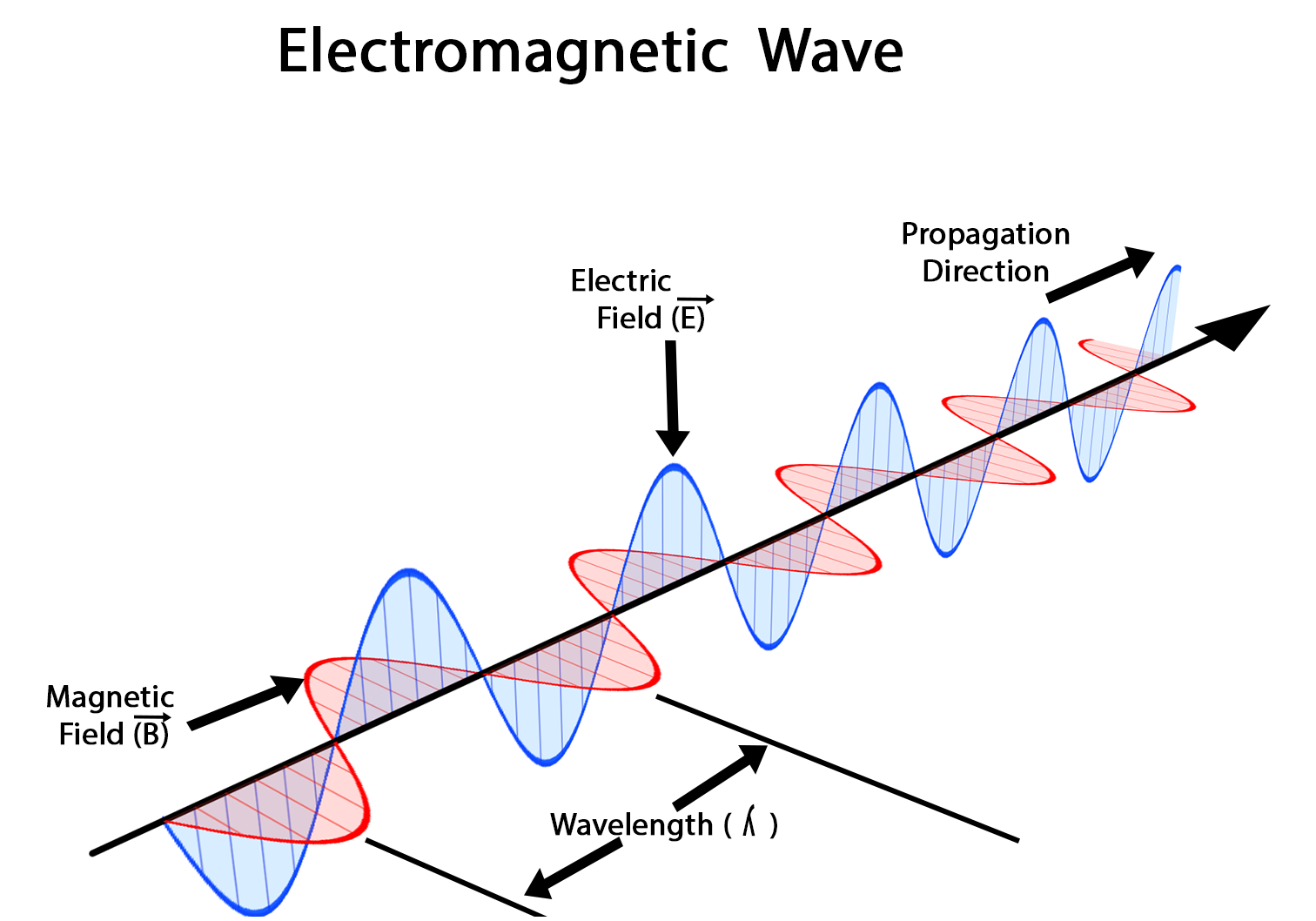
- Propagam-se com a MESMA velocidade: \(c=299,8 mil km/s\).
Radiação Eletromagnética
Espectro Eletromagnético
- Radiação Eletromagnética unifica diversos fenômenos:
- Luz, Infravermelho, Ultravioleta, Ondas de Rádio, Microondas, Raios X, Raios Gama.
- Todos são Radiação Eletromagnética - mudando apenas a frequência!!
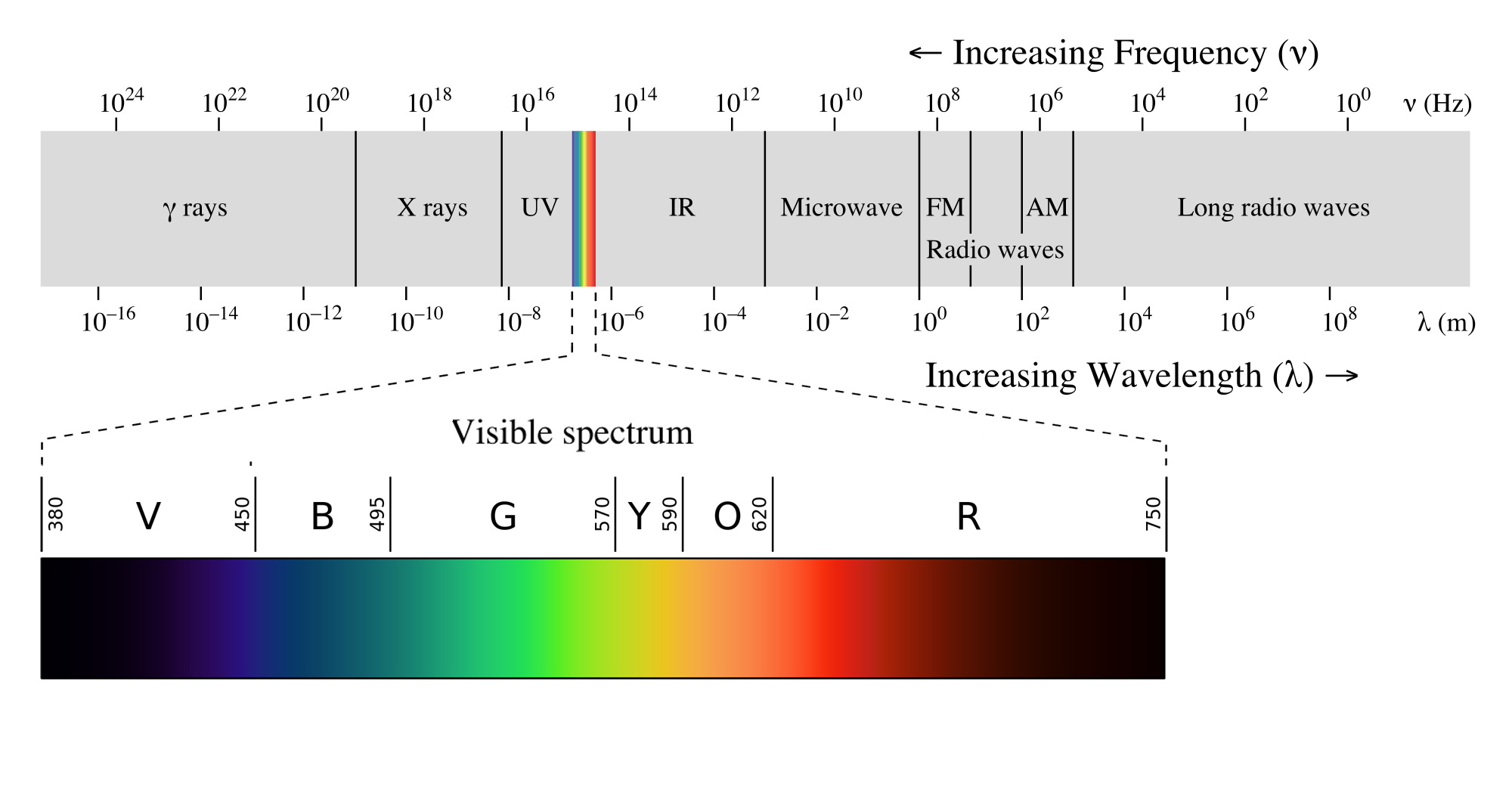
Radiação Eletromagnética
Quanta de Luz - Na virada do Século XIX para XX:
- Descobriu-se (Planck) que a Energia da luz estava ligada a sua frequência:
\[ E = \frac{hc}{\lambda} = h \nu,\] onde \(h=6,626\times 10^{-34}\)Js, \(\lambda\) é o comprimento de onda (m), \(\nu\) é a frequência (Hz), e \(c\) é a velocidade da luz \(c=299,8\) mil km/s = \(2,998x10^8\)m/s (decorar: 300 mil kilômetros por segundo!).
Einstein explicou o Efeito Fotoelétrico.
Unidades comuns para \(\lambda\): mm (rádio), \(\mu\)m (microondas-IV), nm (visível-UV).
Radiação Eletromagnética
Divisão do Espéctro:
- UVC (100-280nm)
- UVB (280-315nm)
- UVA (315-400nm)
- Visível (400-700nm)
- IV próximo (0,78-3,5)\(\mu\)m
- IV termal (3,5\(\mu\)m-1mm)
- Radiação Solar abrange TODO o espéctro, no entanto é mais intenso no visível e UV, indo a zero para \(\lambda > 4\mu\)m.
Ângulo Sólido
O que é
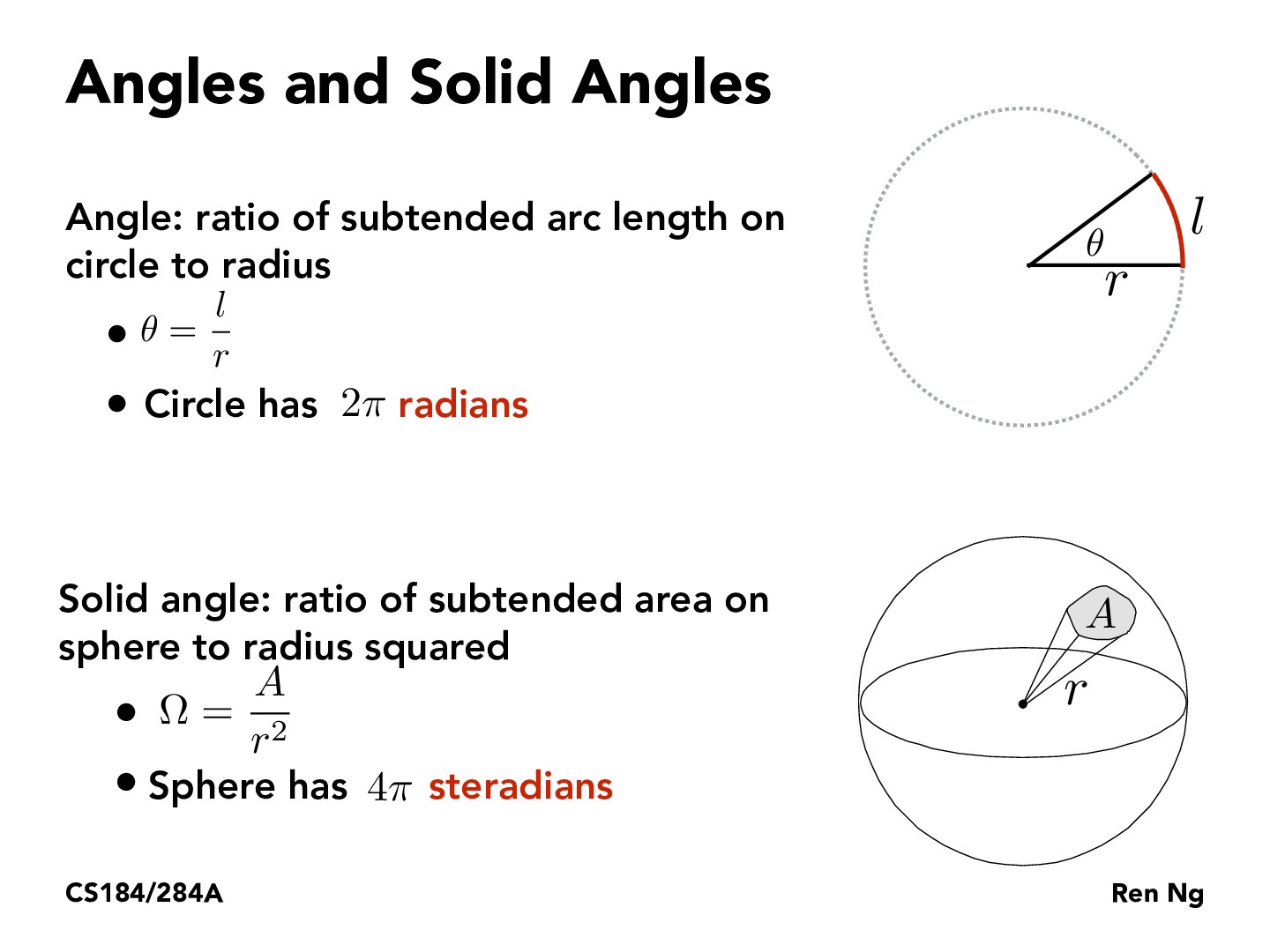 * Unidade: steroradiano (sr).
* Unidade: steroradiano (sr).
Ângulo Sólido
Coordenadas esféricas
- Calota infinitesimal: \(d\sigma = r d\theta r \sin(\theta) d\phi\).
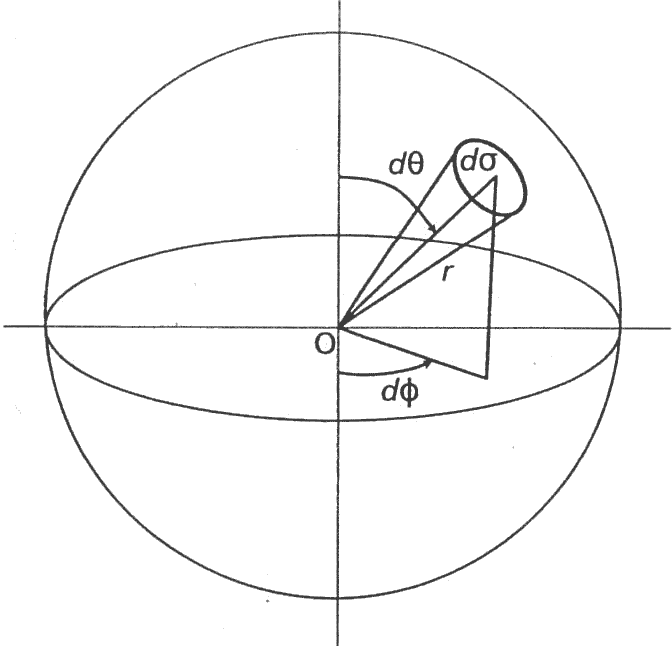
Ângulo Sólido
- Ângulo sólido: \(\Omega=\frac{S}{R^2} = \sin(\theta) d\theta d\phi\).
No caso de Latitude e Longitude:
- Ângulo sólido: \(\Omega=\frac{S}{R^2} = \cos(lat) dlat\,dlon\).
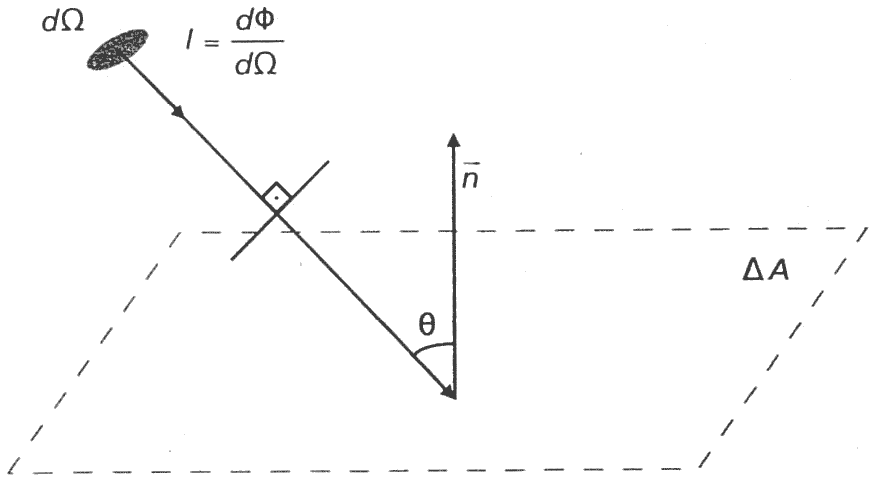
Fluxo, Intensidade, Irradiância e Radiância
Fluxo
- Fluxo de energia = energia que passa por segundo (potência) \[ \phi = \frac{Q}{T} = \frac{dQ}{dt}.\]
- \(Q\) - energia radiante (J).
- \(\phi\) - fluxo de energia (W).
- \(T\) - tempo considerado.
Intensidade Radiante
- De uma fonte puntual em uma determinada direção:
- O fluxo de energia dividido pelo ângulo sólido de propagação dessa radiação: \[ I=\frac{\phi}{\Omega} = \frac{d\phi}{d\Omega}.\]
Fluxo, Intensidade, Irradiância e Radiância
Irradiância
Em um determinada area em uma superfície: \[ E=\frac{d\phi}{dA}.\]
Ex. A radiação solar atinge a superfície da Terra com irradiância de \(1,3\mathrm{kW/m}^2\).
Fluxo, Intensidade, Irradiância e Radiância
Radiância
- Em uma dada direção, em um dado ponto (área) de uma superfície:
- A razão entre a intensidade radiante emitida pela área ortogonal insidente: \[ L=\frac{dI}{\cos{\theta}dA} = \frac{d^2\phi}{\cos{\theta}dAd\Omega}.\]
- Ou a razão da Irradiância pelo ângulo sólido: \[ L=\frac{dE}{\cos{\theta}d\Omega}.\]
Fluxo, Intensidade, Irradiância e Radiância
Fluxo, Intensidade, Irradiância e Radiância
Radiância - Irradiância
- Outra maneira de definir Irradiância
- Integral da radiância (L) pelo ângulo sólido: \[ E = \int L \cos{\theta} d\Omega = \int_{\theta_i}^{\theta_f} \int_{\phi_i}^{\phi_f} L \cos{\theta} \sin{\theta}d\theta d\phi.\]
Para a esfera total: \[ E = \int_S L \cos{\theta} d\Omega = \int_{0}^{\pi} \int_{0}^{2\pi} L \cos{\theta} \sin{\theta}d\theta d\phi.\]
Número de Onda
Onda Senoidal
\[f(x,t) = A \sin{\left(\frac{2\pi}{\lambda}(x-vt)\right)} = A \sin{\left(2\pi(kx-\nu t)\right)},\] onde \(k = \frac{1}{\lambda}\) e \(\nu = \frac{1}{T}\).
- \(\nu\) é a frequencia (Hz = 1/s)
\(k\) é o número de onda (1/m ou comumente 1/cm).
Ex. Uma onda de comprimento de onda \(\lambda=1mm\) qual é o seu número de onda? $ 1) Quantas ondas cabem em 1cm? Resp = 10. 2) Então o Número de onda é \(k=10\mathrm{cm}^{-1}\).
Exercícios:
- Calcule a frequencia de oscilação de:
- Ondas de rádio: \(\lambda=1cm\)
- Microondas: \(\lambda=1mm\)
- Infravermelho; \(\lambda=10\mu\)m
- Visível verde
- UVA
- Mostrar que o ângulo sólido de uma esfera é \(4\pi\).
Calcule o ângulo sólido de um retângulo de 1°x1° (lat/lon) na linha do equador.
A irradiância solar tem um valor de \(1,3\)kW/m\({}^2\). Calcule quanta energia pode ser captada por um painel solar de \(2\mathrm{m}^2\) durante o período de uma hora ao meio dia, assumindo uma eficiência de 30%.
Provar que, se a radiação for isotrópica, ou seja, a radiância é a mesma em todas as direções (constante igual a \(L\)), a irradiância total incidente em um hemisfério é igual a \(\pi L\).
Calcule o Número de onda de uma onda com \(\lambda=10\mu\)m, \(1\mu\)m e 100nm. Em unidades de 1/cm.
Densidade Espectral
- Normalmente a radiação não é monocromática, se espelha em uma região do espéctro.
- Ex. A radiação de uma lâmpada incandescente abrange tando o visível quanto o infravermelho!
- Densidade Espectral: a taxa de radiância emitida por cada comprimento de onda:
\[ L(\lambda) = L_\lambda = \frac{\Delta L}{\Delta \lambda}=\frac{dL}{d\lambda}, \]
- Unidades: \(\mathrm{W/m^2/sr/cm}\)
Densidade Espectral
A densidade espectral pode ser em termos da Frequência ou do Número de onda - basta converter a derivada (regra da cadeia) usando: \[ c = \lambda\nu \rightarrow \nu = \frac{c}{\lambda} \rightarrow d\nu = \frac{c}{\lambda^2}d\lambda \rightarrow \frac{1}{d\lambda} = \frac{c}{\lambda^2}\frac{1}{d\nu}. \]
- Densidade em termos da frequência: \[L_\nu = \frac{dL}{d\nu} = \frac{dL}{d\lambda} \frac{\lambda^2}{c}.\]
Densidade em termos do número de onda \[L_k = \frac{dL}{dk} = \frac{dL}{d\lambda} \lambda^2\].
Espalhamento, Absorção e Transmissão
- O fluxo de radiação Eletromagnética (\(\phi\)) incidente na matéria sofre:
- Atenuação: processo de absorção parcial ou total da energia luminosa pela matéria.
- Emissão: processo onde a matéria emite energia radiante aumentando o fluxo.
- Espalhamento: processo onde a luz é redirecionada (para várias direções) pela matéria.
- Esses três processos físicos podem ser resumidos em três parâmetros:
- Absorção: \(\alpha = \frac{\phi_{abs}}{\phi}\).
- Reflexão: \(\rho = \frac{\phi_{refl}}{\phi}\).
- Transmição: \(\tau = \frac{\phi_{trans}}{\phi}\).
- Esses coeficientes são SEMPRE função do comprimento de onda.
Espalhamento, Absorção e Transmissão
- Cada um desse pode acontecer em certa fração:
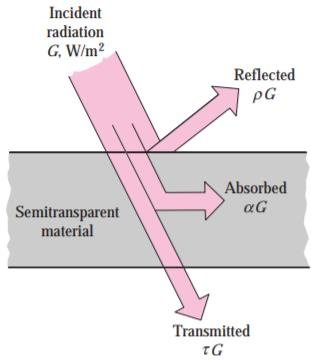
Espalhamento, Absorção e Transmissão
- Absorção da radiação solar como função do comprimento de onda.
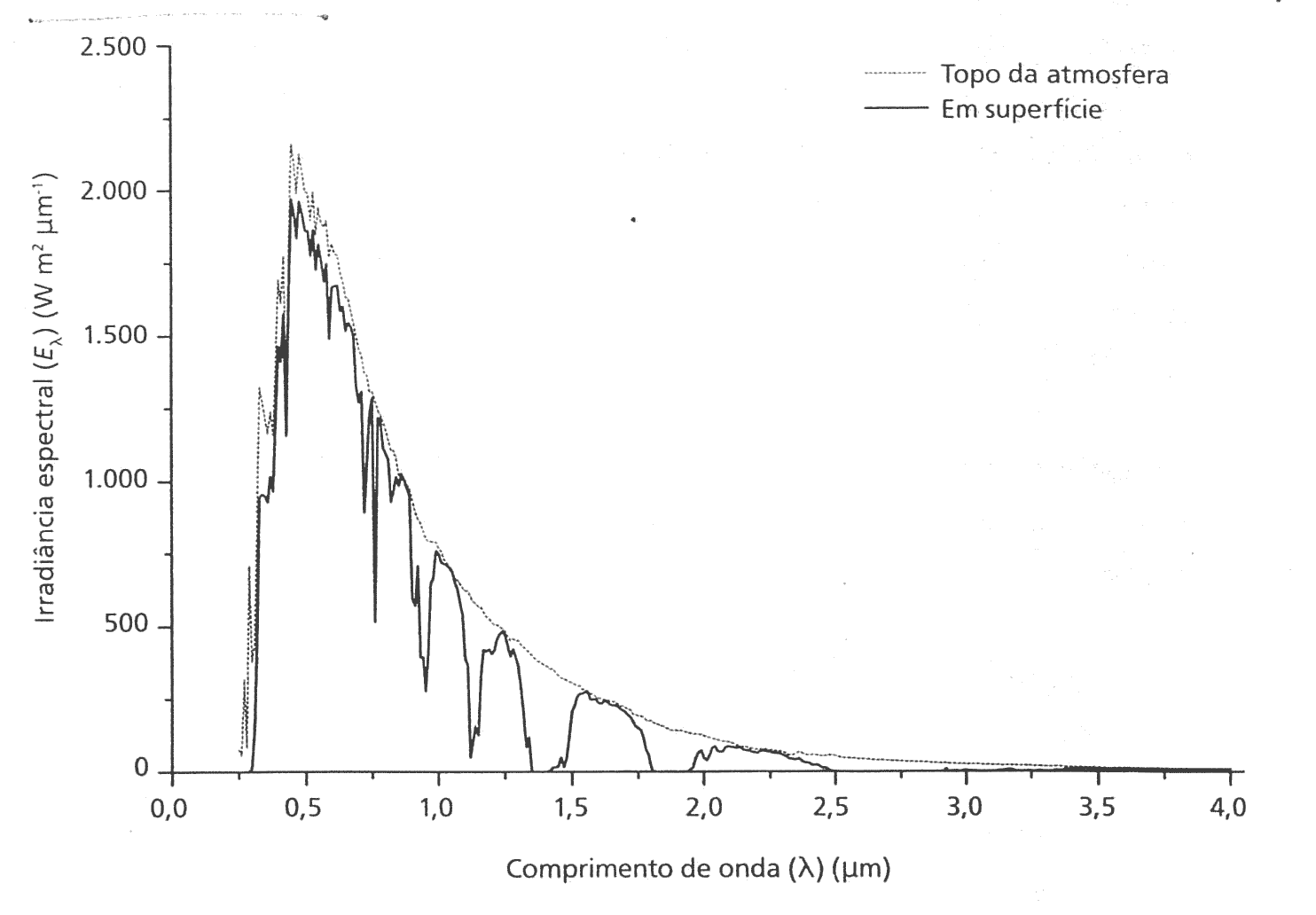
Espalhamento, Absorção e Transmissão
- Por conservação de energia:
- Energia incidente (\(E_{tot}\)) é dividida em três partes (\(E_\rho\), \(E_\tau\), \(E_\alpha\)), ou seja:
\[ E_{tot} = \rho E_{tot} + \tau E_{tot} + \alpha E_{tot},\] ou \[ \rho + \tau + \alpha = 1. \] 
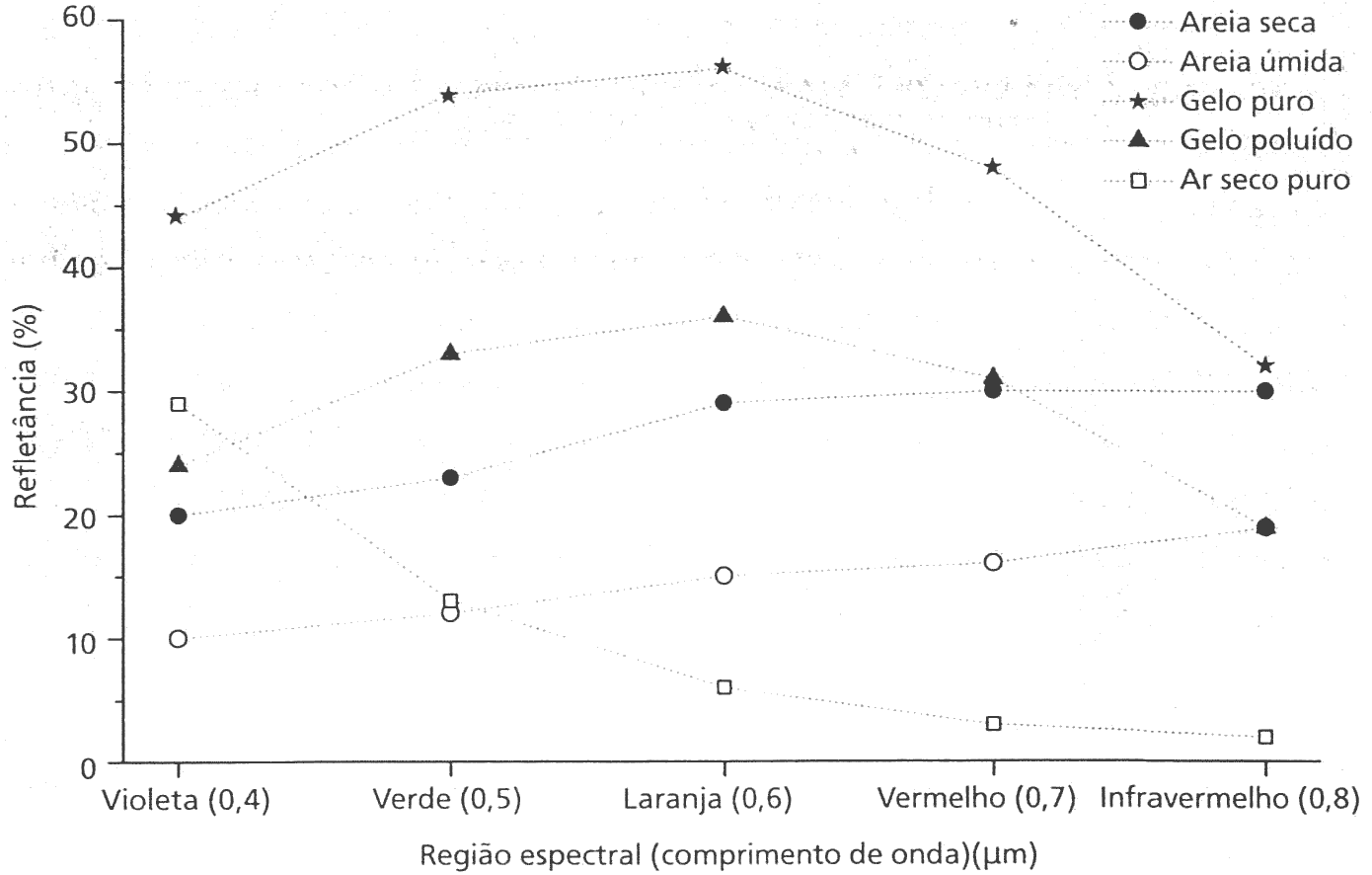
Reflectância - Areia (curtas: \(\lambda<4\mu m\))
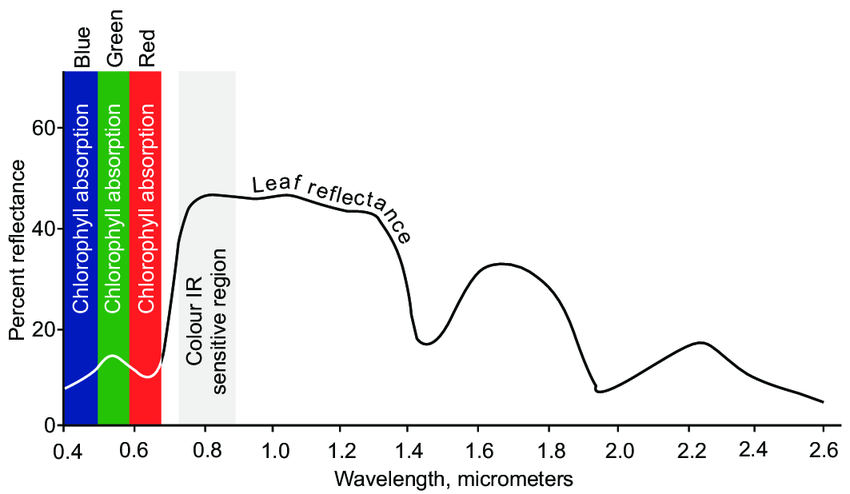
Reflectância - Folha sadia (curtas: \(\lambda<4\mu m\))
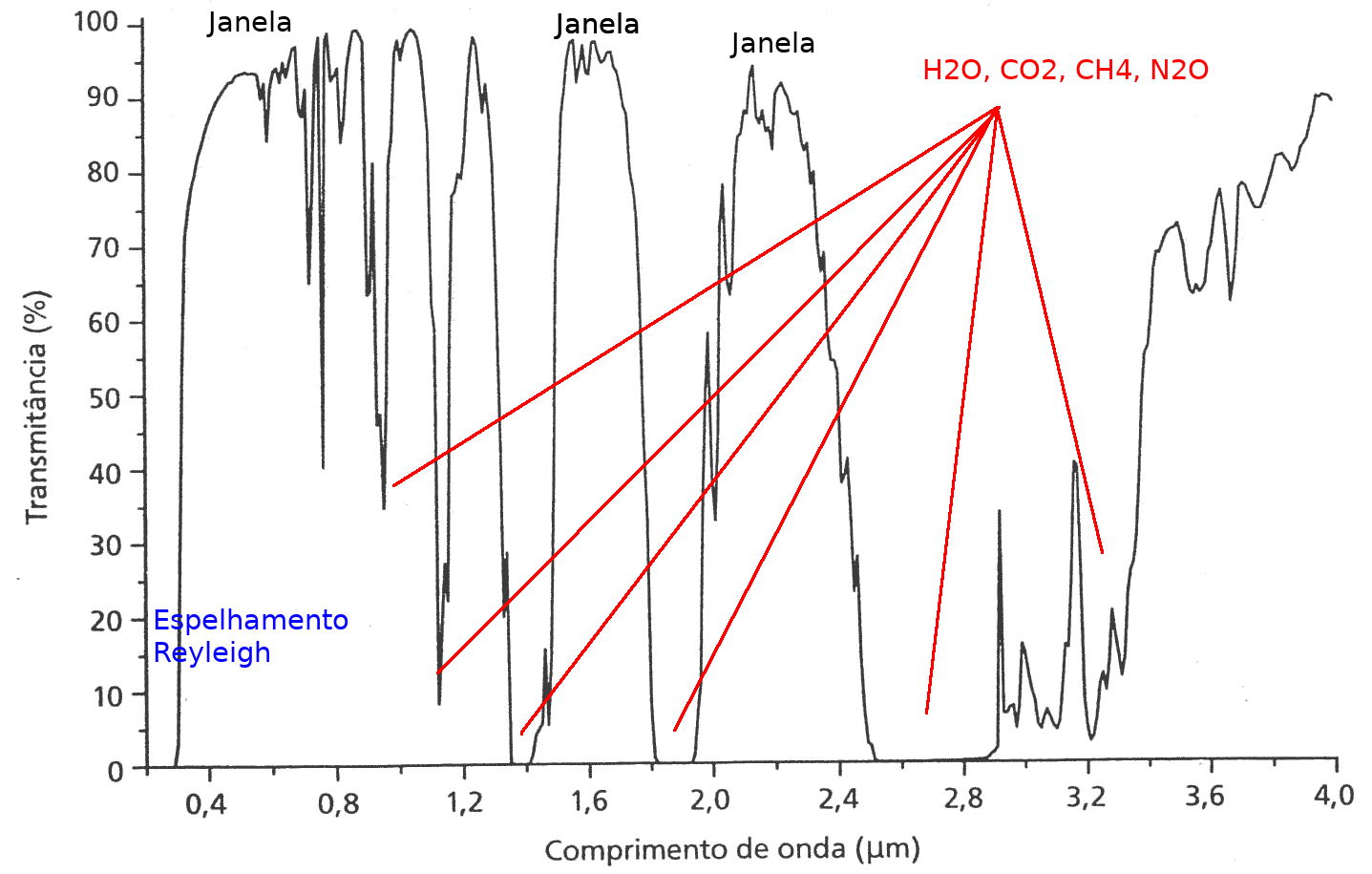
Transmitância - Atmosfera (curta)
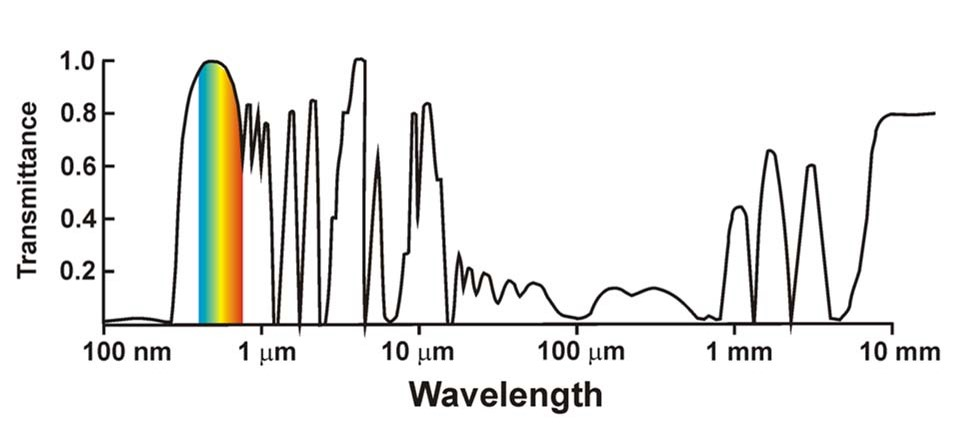
Transmitância - Atmosfera (curta e longa)
Exercícios
Uma folha sadia tem sua reflectância definida como nos slides acima. Calculo o NDVI de uma folha sadia: \[ \mathrm{NDVI} = \frac{|R_{\mathrm{IR}}-R_{\mathrm{RED}}|}{|R_{\mathrm{IR}}+R_{\mathrm{RED}}|}, \] onde RED tem \(\lambda = 700nm\) e IR tem \(\lambda = 1.0 \mu m\).
Imagine que voce tem observações de uma cena onde a luz é separada em cores do espectro. Usando o quadro de reflectância da areia e gelo, como voce poderia distinguir entre os dois? Ou seja, que comparação de cores (e IR) voce poderia usar para disinguir entre eles?
Radiação de Corpo Negro
- Corpo negro
- "algo muito preto!"
- Algo que absorve a 100% da radiação, sem reflexão ou transmissão.
- Mas o que acontece com a energia absorvida? (imagine o corpo negro como uma um corpo oco com um pequeno furinho)
- A energia fica dentro! \(\rightarrow\) Esquenta! e ai?
Corpo Negro - Lei de Kirchhoff
- Vamos assumir o "Equilíbrio Termodinâmico"
- (uma maneira bonita de dizer: vamos esperar bastante tempo até que as coisas parem de mudar!)
- Se está em equilíbrio: \(E_\mathrm{entra} = E_\mathrm{sai}\).
- Tembém equilíbrio mecânico, quimico, ...
- Mas de que fora emite energia pra fora? Qual a emissão de energia?
- Um fato da física experimental:
- Quem absorve bem (reflete pouco, algo escuro) emite bem.
- Quem absorve mal (reflete muito, algo claro) emite mal.
Lei de Kirchoff
- Lembrando: um corpo absorve radiação, em cada comprimento de onda, de acordo com sua absortância (coeficiente de absorção), \(\alpha_\lambda\).
- A razão entre a energia emitida e o coeficiente de absorção, é uma função universal, \(E_\lambda/\alpha_\lambda=B(\lambda,T)\), que depende apenas de \(\lambda\) da Temperatura do corpo.
- Definindo a Emissividade \(\epsilon_\lambda\) como: \(E_\lambda = \epsilon_\lambda B(\lambda,T)\)
- Lei de Kirchhoff: \[ \epsilon_\lambda = \alpha_\lambda. \]
- por definição \(\epsilon = 1\) para o Corpo Negro ideal.
- Tem outros valores para corpos reais.
- Ainda não sabemos o que é \(B(\lambda, T)\) ainda!
Lei de Kirchoff
- Note:
- A lei de Kirchhoff vale quano temos Equilíbro Termodinâmico!
- Em materiais, é necessário haver colisões moleculares suficientes para haver troca de energia.
- No ar, próximo a superfície, essa troca ocorre rapidamente e diz-se que se está em Equilíbrio termodinâmico.
- Acima de \(\approx\) 40km de altitude, o ar já se torna bastante rarefeito e neste caso o equilíbrio termodinâmico NÃO OCORRE.
- Em altas atitude tem-se que se considerar processos radiativos físicos fora do equilíbrio termodinâmico - importante para CO2 na região de 4\(\mu\)m.
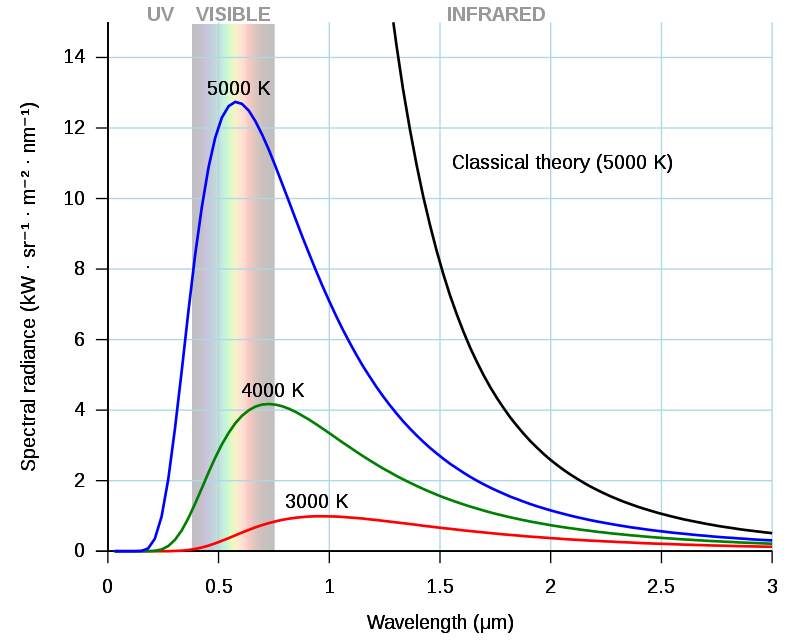
Lei de Planck
- Qual é a forma de \(B(\lambda, T)\)?
- Em 1901, Planck tentando encontrar uma expressão para \(B\) notou que:
- Só é possível se a energia for transferida em parcelas fíxas de energia (os quanta de energia)
- \(E = h\nu\), \(h=6,626\times 10^{-34}\)Js, é a constante de Planck.
- A lei de Planck, em função da frequencia \(\nu\) é:
\[ B(\nu,T) = \frac{2h\nu^3}{c^2\left[\exp{\left(h\nu/kT\right)}-1\right]}, \]
em [W/m²/sr/Hz].
Lei de Planck
- Ou, em termos de comprimento de onda: \[ B(\lambda,T) = \frac{2hc^2}{\lambda^5\left[\exp{\left(hc/\lambda kT\right)}-1\right]}, \] em [W/m²/sr/\(\mu\)m].
Lei de Planck - Wein e Stefan-Boltzmann
- À partir de Planck, pode-se derivar duas leis que já eram conhecidas antes:
Wein - o ponto máximo da radiância: \[ \lambda_\mathrm{max} = \frac{2.897}{T}.\]
Segunda lei de Wein - Radiância máxima: \[ B(\lambda_\mathrm{max},T) = K T^5.\]
Stefan-Boltzmann - Radiância Total emitida (integrada em todas as frequencias): \[ B(T) = \sigma T^4 = \frac{2\pi^4k^4}{15h^3c^2} T^4, \] onde \(\sigma=5,67\times 10^{-8} \mathrm{W/m^2/K^4}\) é a constante de Stefan-Boltzmann.
Um corpo REAL tem uma emissividade média \(\epsilon\) e a sua emissão total é: \[E(T) = \epsilon \sigma T^4. \]
Exercícios
Obter a expressão da radiância espectral de um corpo negro em função do númedo de onda.
Calcular o comprimento de onda de máxima emissão para um ser humano, T=37C, e para o Sol, T=5500C. Em qual banda do espectro encontram-se esses máximos de emissão?
Derivar a lei de Wein.
Derivar o valor de K na segunda lei de Wein.
Exercícios
Radiação na Atmosfera
- Prof. Breno Imbiriba
- Periodo especial da PANDEMIA - 2020
- Aula 3 - RADIAÇÃO SOLAR - 7/out/2020
O Sol - Características
- A nossa estrela! (amerela)
- Distância média de 150 milhões de kilômetros: \(\bar{d}\approx 149597872km\) = 1 UA (Unidade Astronômica)
- 1 UA \(\approx 150\times 10^6\)km \(\approx 1,496\times 10^{11}\)m.
- 1 UA = 4 minutos-luz.
O Sol - Geometria
O Sol - Geometria
- Mas a órbita da Terra é elíptica:
- Periélio \(d=147,1 \times 10^6\)km.
- Afélio \(d=152,1 \times 10^6\)km.
- Variação de 3%.
- Forma esferoidal com raio de \(R=696,3\) mil km (a Terra tem raio 6,3 mil km).
- Massa \(M=1,99\times 10^{30}\) kg. (\(M_\mathrm{Terra}=5,97\times 10^{24}\));
- 75% hidrogênio e hélio, o resto são elementos mais pesados.
- Energia vinda da fusão nuclear no seu núcleo (Hidrogênio para Hélio, e outros elementos).
O Sol - Radiação
- Empiricamente, chega no planeta Terra (no topo da atmosfera - TOA) a irradiância total solar de: \[ E_0 = 1366 \mathrm{W/m^2},\] chamada constante solar.
- Essa constante não é bem constante! Varia em cíclos de 11 anos (e outros períodos).
- Antes das medidas de satélite estimava-se em 1361W/m\({}^2\). (o que é uma questão!!)
O Sol - Manchas solares (histórico)
O Sol - Irradiância
O Sol - Radiação
- Estimativa teórica da constante solar:
- A Fluxo de Energia (potência) total do Sol: \(\phi_s=3,9\times 10^{26}\)W.
- A Irradiância Emitida (Pot/Area) é \[E_s=\frac{\phi_s}{A_s}=\frac{\phi_s}{4\pi R_s^2} = \frac{3,9\times 10^{26}}{4\pi(7\times 10^8)^2} = 6,3\times 10^7\mathrm{W/m^2}.\]
- Essa irradiância total se espalha pelo espaço uniformemente até atingir a Terra, na diatância de 1UA: \[\phi_s=\phi_0\rightarrow E_s4\pi R_s{}^2 = E_04\pi d^2\rightarrow \] \[E_0=\frac{6,3\times 10^7(7\times 10^8)^2}{1,5\times 10^{11})^2} = 1372\mathrm{W/m^2}.\]
O Sol - Radiação
O Sol - Radiação
- Quando a Terra se afasta ou se aproxima do Sol, a irradiância incidente total varia de acordo com: \[E(d) = \left(\frac{\bar{d}}{d}\right)^2E_0.\]
- Isso é sobre uma superfície PERPENDICULAR aos raios solares (meio-dia!)
- Exercício 2 - Demonstre essa fórmula.
- Exercício 3 - Determinar \(E(d)\) para \(d=0,95\bar{d}\) e \(d=1,02\bar{d}\).
- Exercício 4 - Se a Terra tambem for um corpo negro, estime o valor da sua temperatura nesses dois casos. (use o fato de que a energia que entre na Terra devido ao Sol é a mesma que sai devido a radiação de corpo negro da Terra, dado pela lei de Stefan-Boltzmann.)
O Sol - Radiação
- Problema:
- No filme "2010" o planeta Jupiter se torna uma estrela. Considere que isso realmente ocorra e ele se torne uma estrela de 6000K. Estime a irradiância total que atingiria a Terra. Assuma que o raio da órbita de Jupite \(R=5,2\)UA, e que o raio de Júpitar seja de 71300km.
O Sol - Radiação
Resolução dos exercícios - 1
Resolução dos exercícios - 1
Resolução dos exercícios - 1
- Então
- Sabemos: \(E_{terra}=1366\mathrm{W/m^2}\),
- \(A_{terra}=\Omega (4\pi \bar{d}^2)\),
- \(A_{sol}=\Omega (4\pi R_{sol}^2)\),
- E resolvemos para \(E_{sol}\). \[E_{sol} = E_{terra} \frac{A_{terra}}{A_{sol}} = 1366\frac{\Omega \bar{d}^2}{\Omega R_{sol}^2}.\]
- Fazendo a conta: \(E_{sol}=6,305\times 10^7\mathrm{W/m^2} = \sigma T^4\).
- Calculando: T=5774K.
Resolução dos exercícios - 2
- A irradiância solar é o fluxo total de energia pela área do esfera que envolve o Sol. \[E_0 = \frac{\phi}{4\pi\bar{d}^2}.\]
- Para uma outra distância, basta mudar o valore de \(\bar{d}\).
- Mas o fluxo é sempre constante: \[ \phi=4\pi \bar{d}^2 E_0 = 4\pi d^2 E_d,\] logo \[ E_d = \left(\frac{\bar{d}}{d}\right)^2E_0.\]
Resolução dos exercícios - 3
- Balanço de Energia - O que chega na Terra é o mesmo que Sai. \[\phi_{entra} = \phi_{sai}.\]
- Na Terra chegam 1366W/m2 = \(\sigma T^4\) e teríamos: T=393K - Muito quente!
- Precisa pensar na GEOMETRIA:
Resolução dos exercícios - 3
- Energia que entra atinge o CÍRCULO de área \(A=\pi R_{terra}^2\).
- Energia que sai, irradia de uma ESFERA de área \(A=4\pi R_{terra}^2\).
- Logo: \[ \phi_{entra} = \phi_{sai} \] \[ E_{entra}A_{disco} = E_{sai} A_{esfera} \] \[ E_0\pi R_t^2 = \sigma T^4 4\pi R_t^2 \] \[ T^4 = \frac{E_0}{4\sigma} = 279K = 6C\].
Resolução dos exercícios - Jupiter
- Dados:
- Distância orbital: 5,2 UA.
- Raio 71300km
- Temperatura: 6000K
- Qual a energia/m2 que atingiria a Terra?
- Menor distância: \(d_j=4,2\)UA.
- \(E_J = \sigma T^4 = 7.348\times 10^7\mathrm{W/m^2}\).
- Fluxo total: \(\phi_J=E_J A_J\).
- Atinge a terra a irradiância \(E_T = \frac{\phi_J}{4\pi d_J^2}\).
- Fazendo a conta: \(E_J=3.95\mathrm{W/m^2}\).
Tamanho Aparente do Sol no Céu.
- Tamanho aparente = ângulo no céu.
- Duas maneiras de calcular (simples e menos simples)
- 1a. Geometria simples \[\tan{(\theta/2)} = \frac{R_{sol}}{d} \qquad \rightarrow \frac{\theta}{2}\approx \frac{R_{sol}}{d}.\]
- Usando os valores: \(R_{sol} = 696340\)km, \(d=1.496\times 10^8\)km, temos: \[ \theta = 0.00931 rad = 0.533^\circ.\]
Tamanho Aparente do Sol no Céu.
Sistemas de Coordenadas
- Para localizarmos objetos no céu precisamod de Sistemas de Coordenadas.
- Aqui veremos três tipos:
- Sistema geográfico.
- sistema Equatorial Horário.
- Sistema Horizontal Local.
- Todos consideram uma esfera imaginária no céu, sobre a Terra.
- A trajetória aparente que o Sol executa no céu chama-se "Eclíptica".
Sistema Geográfico
- A Terra é considerada estática.
- Coordenadas são Latitude (\(\phi\)) e Longitudes (\(\lambda\)) usuais.
Sistema Equatorial Horário
- É um sistema local, ou seja, as medidas são com relação a posição do observador.
- O Ângulo Horário (\(H\)) é a distância angular do meridiano local até a posição do astro.
- Note: Um objeto sobre o meridiano local estará exatamente na posição vertical sobre o observador (meio-dia solar).
- \(H\) é medido sobre o Equador Celeste.
- \(H\) pode ser medido em graus ou em horas (1h=15\({}^\circ\)).
- \(H<0\) de manhã (a leste do meio-dia solar).
- \(H>0\) a tarde (a oeste do meio-dia solar).
- A segunda coordenada é a "Declinação" (\(\delta\)), e é uma longitude, contada a partir do equador celeste.
- \(\delta\) varia entre -90 e 90 graus.
Sistema Equatorial Horário
Sistema Horizontal Local
- Este é um sistema local.
- O Zênite é o ponto na esfera celeste imediatamente a cima, na vertical do observador.
- O oposto do zênite é o nadir, o ponto imediatamente a baixo.
- O plano horizontal (o horizonte) define a parte visível da abóbada celeste, com zênice bem no seu centro.
- O Azimute (\(\phi\)) é a distância angular, na horizontal, entre a direção Norte e a direção do astro.
- Indo de Norte para Leste. O Azimute varian entre 0 e 360 graus.
- A Elevação (\(h\)) é a distância angular, na vertical, entre o horizonte e a posição do astro.
- A Distância Azimutal (\(\zeta\)) é o complemento da elevação: a distância angular entre o zênite e o astro, descendo nesses meridianos.
Sistema Horizontal Local
Radiação na Atmosfera
- Prof. Breno Imbiriba
- Periodo especial da PANDEMIA - 2020
- Capítulo 4 - Medição de Irradiância - 7/out/2020
Radiação de Ondas Curtas
- Radiação Solar - 0,3\(\mu\)m a 4,0\(\mu\)m.
- Devido à emissão de corpo negro do Sol (T=5700K).
- Direta Solar (\(E_s\))
- Raio direto do Sol
- depende só do \(\cos(\zeta)\) e de constituentes atmosféricos
- Difusa (\(E_d\))
- Vinda de TODO O CÉU
- Espalhamento por gases, partículas, núvens...
- Reflexão.
- Irradiância global \(E_g\) é: \[ E_g = E_s + E_d\]
Lei de Beer
- Depende da "Transmitância" da atmosfera: \[E_s = E_0 t_d,\] \(t_d\) é a transmitância direta (fração do feize incidente que não é absorvido ou espalhado).
- Modelada pela "Lei de Beer":
- para um comprimento de onda \(\lambda\), \[t_d(\lambda) = e^{-\tau(\lambda)/\cos(\zeta_0)},\] onde \(\tau(\lambda)\) é a "profundidade óptica".
Exercício 4.1
Um balão meteorológico está localizado a 8km de altitude, onde a profundidade óptica relativa ao topo da atmosfera vale 0,03. Um sensor nesse balão mede a radiância monocromática de comprimento de onda \(\lambda\), perpendicular ao sensor, de \(2,0\mathrm{W/m^2/sr/\mu m}\). Na superfície, um fotômetro acaba de medir a profundidade óptica total da atmosfera (para o mesmo comprimento de onda) com valor 0,19. Determinar a radiância espectral: 1. Indicente no topo da atmosfera. 2. Na superfície.
Exercício 4.2
A radiância espectral de \(875\mathrm{W/m^2/sr/\mu m}\) foi medida com um fotômetro solar no instante em que a elevação do Sol era de 35°. A radiância incidente no topo no mesmo comprimento de onda era igual a \(2000\mathrm{W/m^2/sr/\mu m}\). Com base nisso, determinar a profuncidade óptica da atmosfera no instante da medição.
Radiação de Ondas Longas
- Radiação Terrestre - 4\(\mu\)m a 100\(\mu\)m.
- Devido à emissão de corpo negro da Terra (T=300K).
- Considera-se isotrópica (igual em todas as direções) - A Terra é grande!
- A atmosfera também emite:
- Radiação vem de baixo pra cima (do solo)
- E de Cima pra baix (do Ar)
- Tem que medir ambas as direçõs (dois fotômetros).
Radiação Total e filtros
- A soma das ondas curtas e longas é a "Radiação Total"
- Medidas normalmente são em bandas de comprimento de onda.
- Apontando radiômetros pra cima e pra baixo mede-se diretamente o saldo de radiação.
- Usando um instrumento de ondas longas:
- pode-se mediar a emissividade da superfície.
- Observar certos constituentes atmosféricos gasosos.
- Usando ondas curtas:
- determinação de constituentes atmosféricos como partículas.
- gases que interagem nas onads curtas
- Estudos em impacto ambiental, poluição atmosférica, agrometeorologia, ...
Radiação Total e aplicações
- Medidas podem ser no céu todo - normalmente para cálculos de balanços.
- Podem ser em ângulos sólidos restritos
- Utilizam colimadores
- Medem a radiação de um ponto específico do céu.
- Exemplo: fotômetro solar: Apontam para o Sol e medem a irradiância apenas desta direção (e estimam a profundidade óptica).
5. Absorção e Espalhamento
- Prof. Breno Imbiriba
- Capítulo 5
- 5/Nov/2020
Absorção e Espalhamento
- Vimos que:
- Absorção remove energia da atmosfera: Energia térmica (normalmente)
- Espalhamento espalha a energia: Radiação difusa.
- Mas como isso ocorre?
- Depende das moléculas e partículas no ar.
- Depende também da Temperatura.
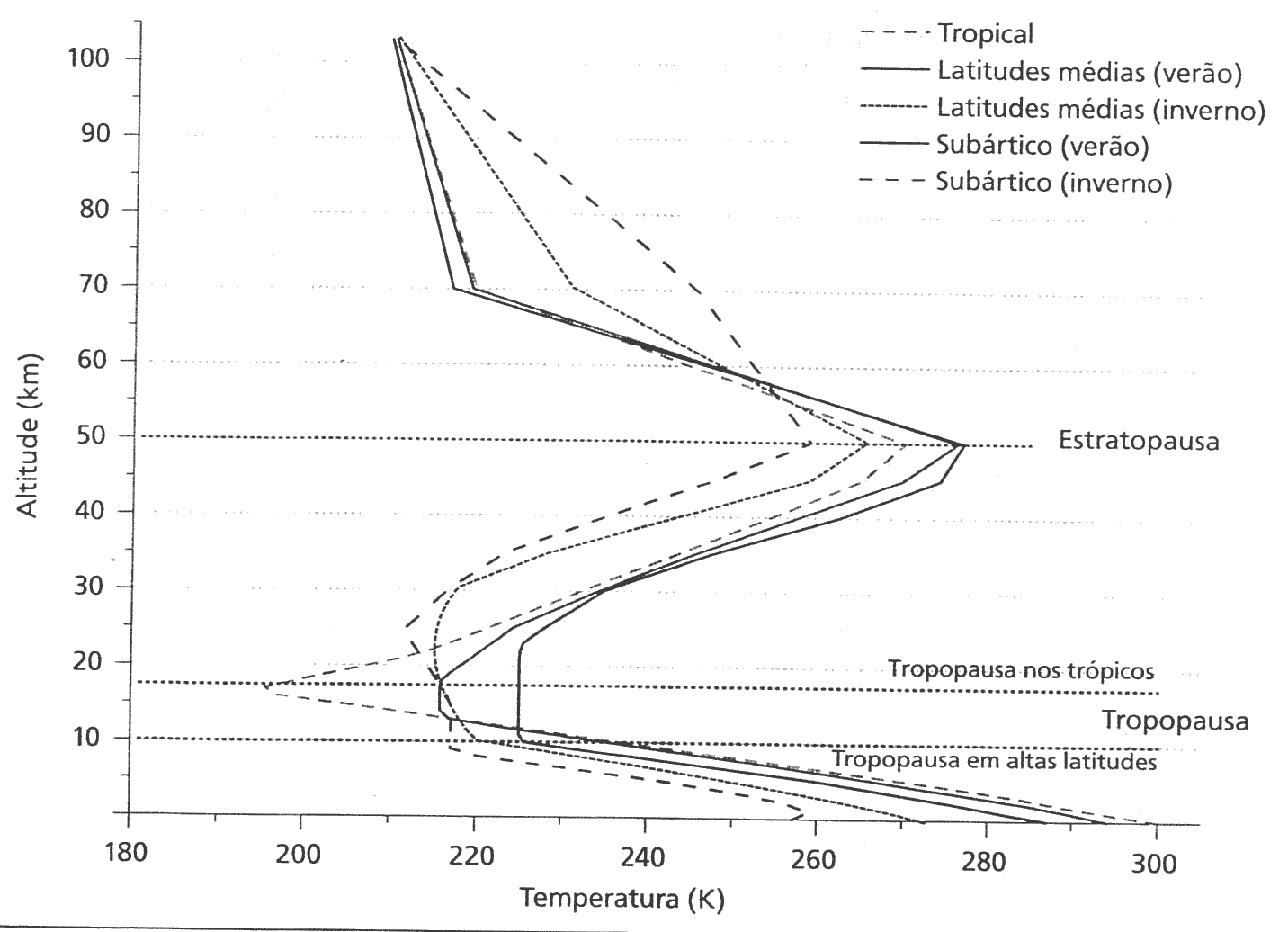
- Perfil de Temperatura:
Perfil de Temperatura:
- Troposfera (aquecimento turbulendo pela superfície).
- 75% da massa de ar, principais eventos meteorologicos.
- Tropopausa (entre 8 e 16km)
- Estratosfera (até 40-50km): aumento da temperatura
- Processos Radiativos: absorção solar na Camada de Ozônio.
- Estratopausa
- Mesosfera (até 90km): resfriação radiativa.
- Mesopausa: Segundo mínimo de temperatura.
- Termosfera (acima de 90km)
- múito tênue (<0,01 mbar)
- Moléculas não se batem
- Aquecimento solar não se dissipa: \(T\approx 800-1200K\).
- Efeitos ionizantes (auroras).
- Tambem chamada de Ionosfera.
Perfil de Temperatura:
Constituentes Atmosféricos
- 0-4% de Água (em volume ou molar).
- Restante seco: 99% N2 e O2.
- O resto:
- Ar - 0,93%
- CO2 - 400ppm = 0,0004% (1%=10000ppm)
- CH4 - 2ppm
- N2O
- O3
- São pouco mas são muito importantes.
- Eles interagem com a radiação eletromagnética.
- Também: Partículas sólidas
- MUITO maiores que as moléculas (\(\approx 1\mu m\)).
Constituentes Atmosféricos - Gases
- N2 - não interage com radiação eletromagnética, porém é precursor de:
- N2O, NO, NO2, HNO3, NH3
- Relevantes em processos biológicos e são gases estufa ou poluentes.
- O2 - não interage com Rad. EM.
- H2O - Maiores concentrações no equador. Forte Gas estufa.
- CO2 - Gas estufa predominantemente antropogênico
- CH4 - Gas estufa predominantemente antropogênico
- O3 - 20-40km - camada de ozônio - absorve UV solar.
- Na baixa troposfera é um poluente nocivo.
- NOx - Predominantemente poluentes urbanos (combustão)
- SOx - Queima de carvão e petróleo. Chuva ácida.
- CFCs/HFC/HCFC
- Antrópico! Ar condicionado.
- Potente gas de efeito estufa.
- Destroi O3! Parcialmente proibido.
Constituentes Atmosféricos - Aerosóis
- Partículas sólidas ou líquidas
- Dispersos na atmosfera
- Vários tipos de composição, forma (morfologia) etc...
- Varios tipos de duração na atmosfera:
- Ex:
- Poeira, cíncas vulcânicas, spray marinho, pólen.
- carbono preto (queimadas),
- certas reções químicas produzem partículas (poluição urbana).
- Tamanho entre 0.01-20\(\mu\)m.
- Mudanças climáticas: Podem esfriar ou esquentar! (depende)
Leiam o Livro!
5.2. Espectro de Absorção e Emissão Atômico
- Cargas elétricas em movimento geram Campos elétrico e magnético.
- Quando estão aceleradas essa cargas geram campos variando no tempo: ONDAS!
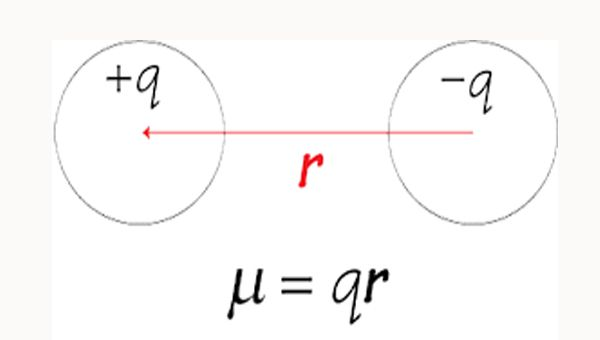
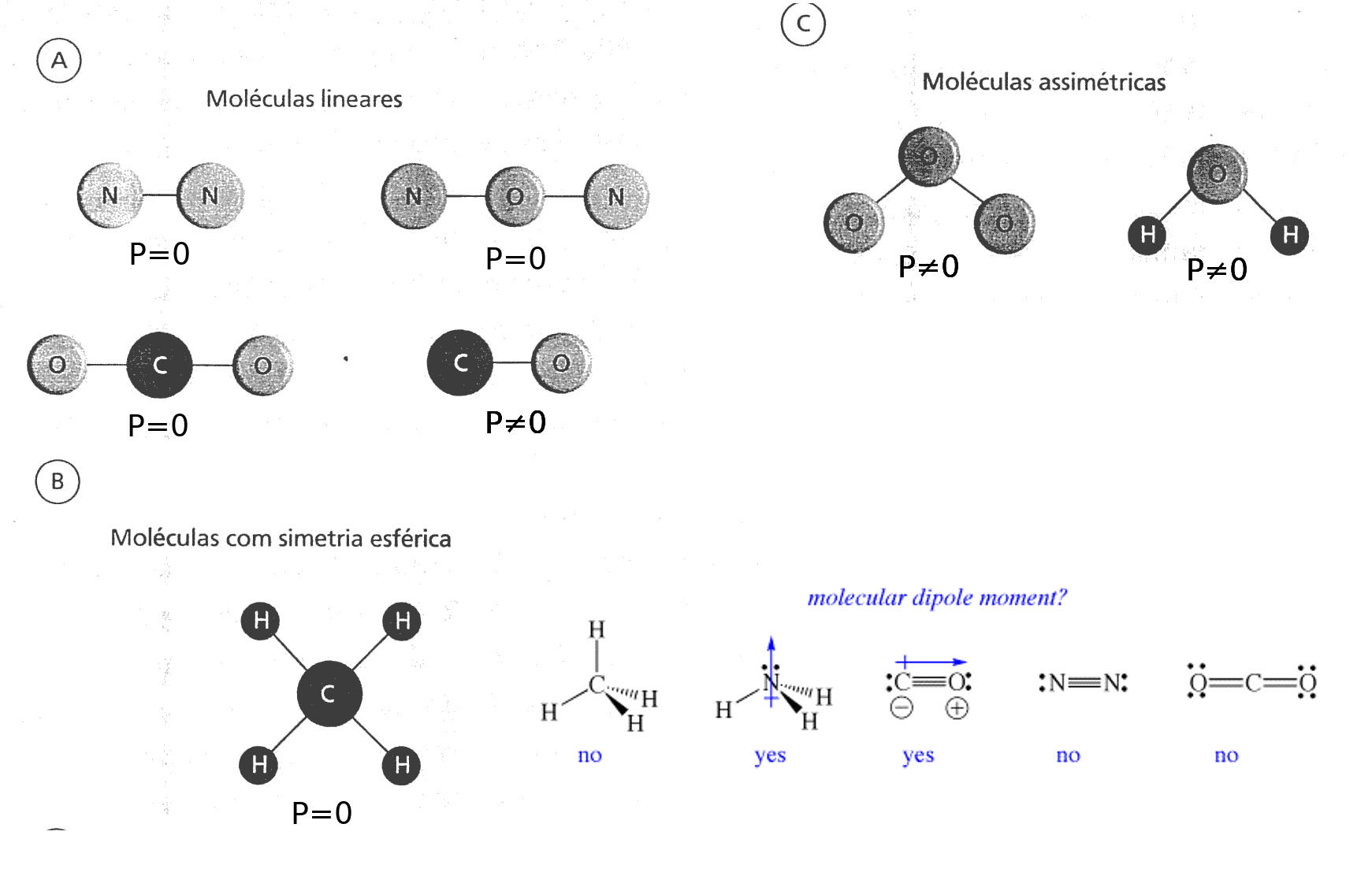
- Lembre-se: Momento de dipolo elétrico:
- Uma medida da polarização de cargas positivas e negativas: \[ \vec{P} = \Sigma_i q_i\vec{x_i},\] ou para duas cargas simétricas: \[ \vec{P} = q_+\vec{x_+}-q_i\vec{x_-} = q(\vec{x_+}-\vec{x_-}) = q\vec{r}.\]
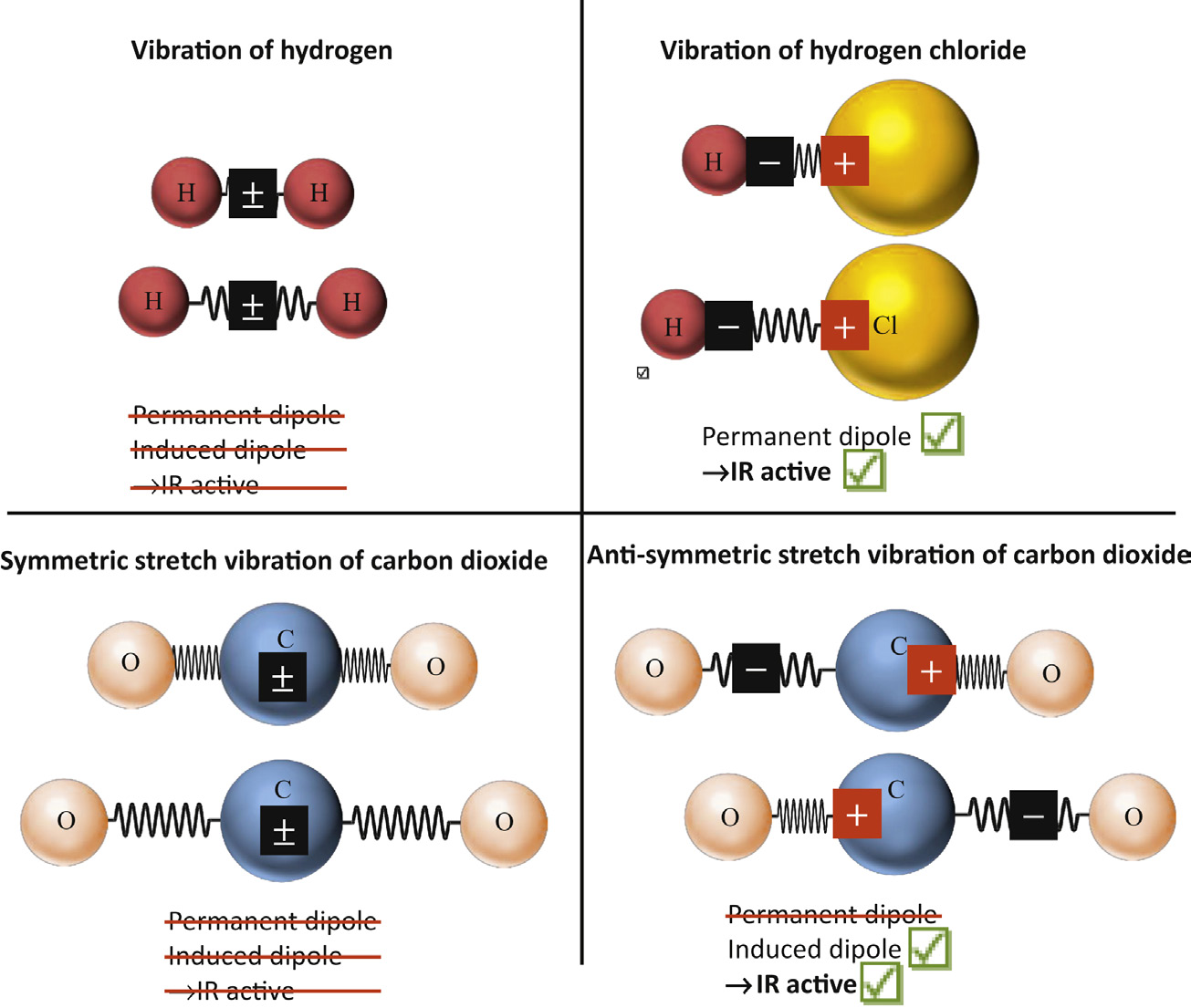
- A radiação só ocorre quando o Momento de Dipolo varia no tempo.
Absorção e Emissão de Radiação Eletromagnética
- Requer alguma mudança de momento de dipolo dos átomos/moléculas.
- As mudanças são chamadas de TRANSIÇÕES, e têm ENERGIA associada a cada uma.
- Elas ocorrem sempre emitindo ou absorvendo radiação eletromagnética.
- Vamos ver três tipos:
- Eletrônica: Elétrons (das eletrosféras dos átomos ou moléculas) mudam de órbita.
- Normalmente emissões no UV/Visível/IR próximo
- Vibração: As moléculas vibram (como massa-mola).
- Ao vibrarem mais rápido ou mais devagar, absorvem ou emitem fóton: IR termal.
- Rotação: As moléculas giram.
- Ao girarem mais rápido, absorvem um fóton. E emitem um fóton para girarem mais devagar. Emissões nas micro-ondas.
- Vibração-Rotação: Infravermelho térmico. Mistura das duas.
Emissão Eletrônica
- Um próton e um elétrom em órbita:
- Eletron livre tem \(E>0\). Elétron em órbita tem \(E<0\).
Emissão Eletrônica
Emissão Eletrônica
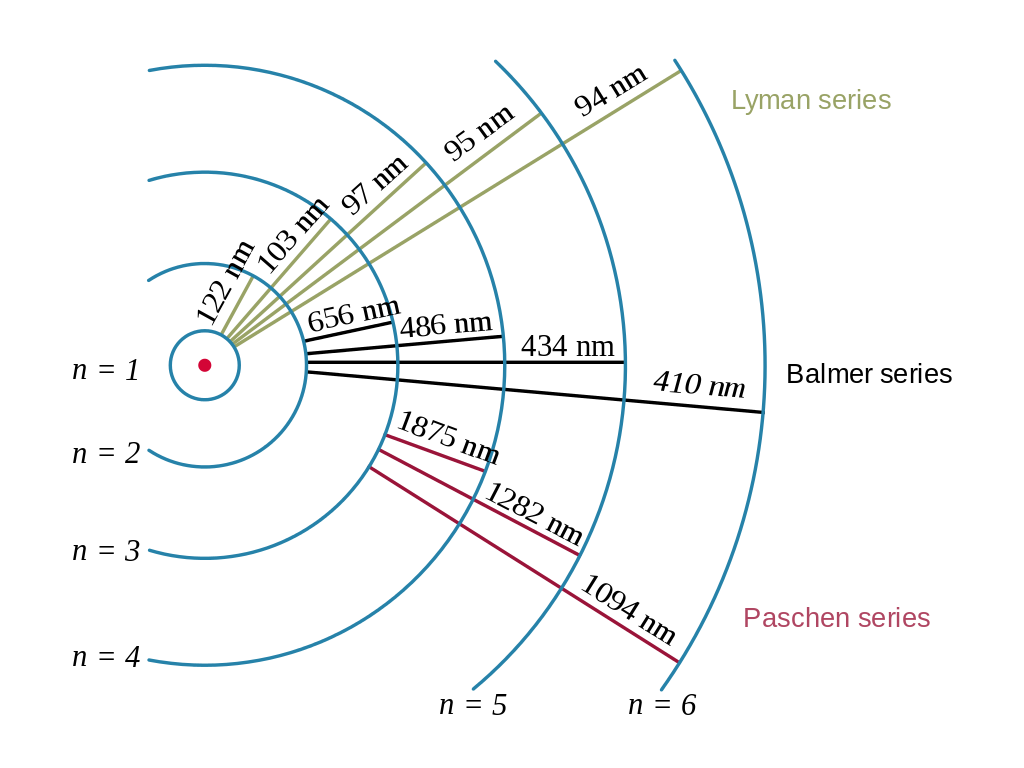
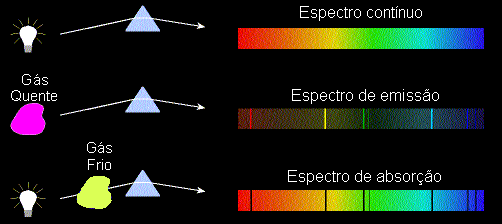
Linhas Espectrais do H - Série de Balmer
- Emissões das transições brilham em uma cor específica
- Passa por um prisma (e por uma janela fina retangular):
- Vermelha, a de menor energia.
- Azul, violeta... maior energia.
- Essas linhas dão o nome Linhas Espectrais.
- Absorção é o processo inverso (as linhas parecem pretas)
Linhas Espectrais: Emissão e Absorção
Emissão por Rotação/Vibração
- Para haver interação com radiação Eletromagética tem que haver mudança em \(P\).
- Algumas moléculas tem \(P=0\) e otras tem \(P\ne 0\).
- Depende da forma das moléculas:
- Lineares
- Simetria Esférica
- Assimétricas
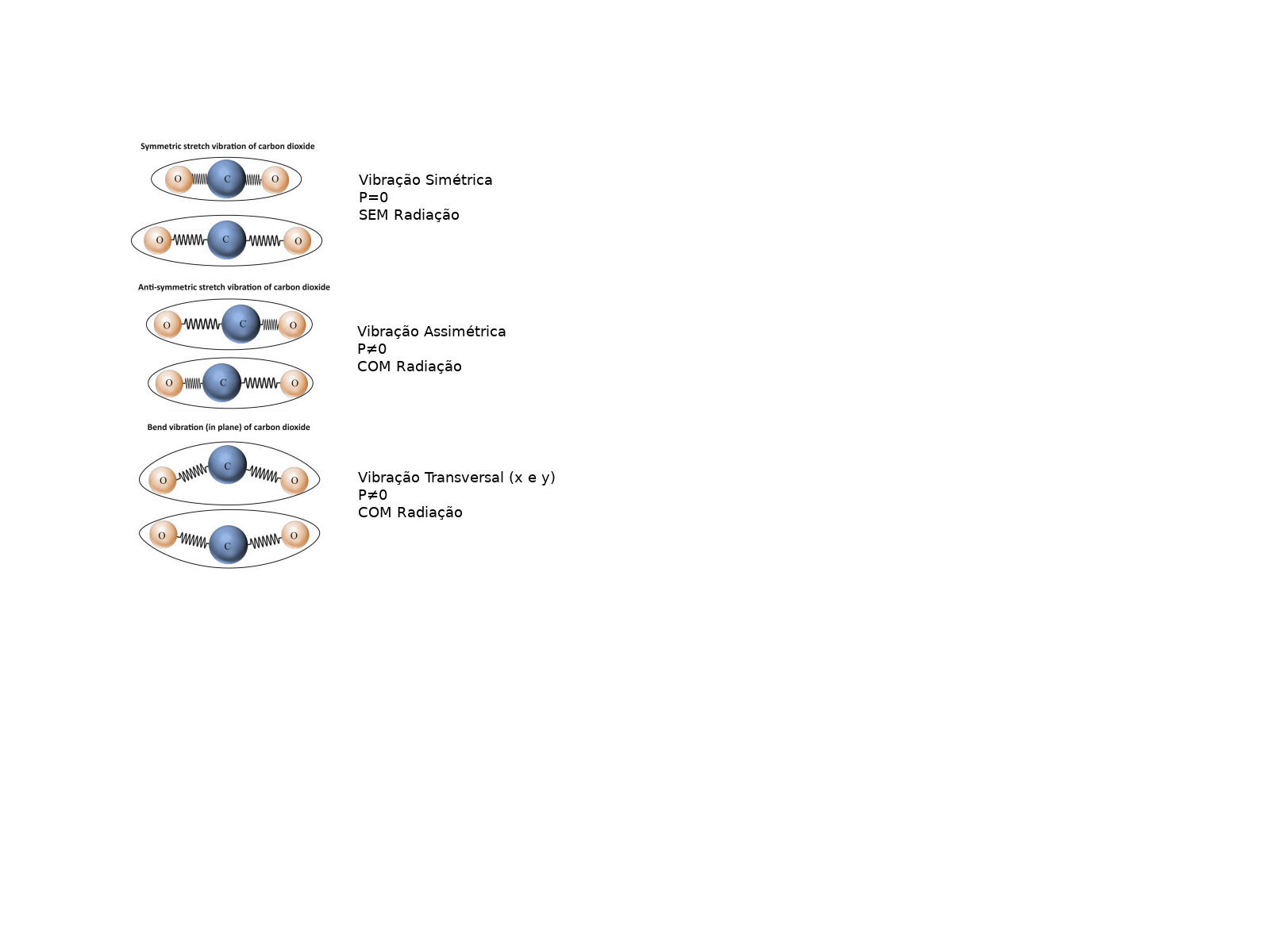
Espectro Vibracional/Rotacional
- Mudança no dipolo elétrico:
Espectro Vibracional/Rotacional
Espectro Vibracional/Rotacional
- Mudança na velocidade de rotação alteram a energia dos fótons emitidos nas transições vibracionais.
- Exemplo: NNO:
Alargamento das Linhas Espectrais
- Elas não são infinitamente finas!
- Tem uma certa largura.
- Modeladas por:
- Lorentz - Alargamento via Pressão
- Colisão entre as moléculas causa variação na posição exata da linha.
- Efeito final é um alargamento da linha.
- Maior quanto maior a pressão: \[\alpha(P,T) = \alpha_0\frac{P}{P_0}\sqrt{\frac{T_0}{T}}.\]
- Approx \(0,01 - 0,1 cm^{-1}\).
Alargamento das Linhas Espectrais
- Doppler - Alargamento via Efeito Doppler
- Às vezes a molécula se afasta do observador, às vezes se aproxima!
- Cada uma então aparenta ter a linha espectral em outra posição. \[ \nu = \nu_0\left(1\pm\frac{v}{c}\right).\]
- Maior efeito quanto maior a velocidade (Temperatura) \[\alpha(T) = \frac{\nu_0}{c}\sqrt{\frac{2kT}{m}}.\]
- Importante para altitudes entre 20km e 50 km (estratosfera).
- Voigt - mistura das duas, para baixas pressões (\(\approx 40km\))
Alargamento das Linhas Espectrais
Alargamento das Linhas Espectrais - Bandas
Coeficiente de massa e Profundidade Óptica de absorção
- Já sabemos das linhas espectrais
- Transições elétronicas e de vibração/rotação que interagem com a radiação EM.
- Um gás quente ENERGIZA as moléculas e elas podem EMITIR, nos comprimentos de onda das linhas espectrais.
Um gás frio pode ABSORVER radiação EM ao passar por ele, nos comprimentos de onda das linhas espectrais.
- Como QUANTIFICAR essa absorção?
Coeficiente de Massa e Profundidade Óptica de Absorção.
Coeficiente de Absorção
- Coeficiente de Absorção definido pela posição, intensidade e forma da linha: \[ k_a(\nu) = S f(\nu-\nu_0)\]
- \(S\) é a intensidade da linha - é a absorção total da linha (cm²/g).
- \(f\) é o perfil da linha:
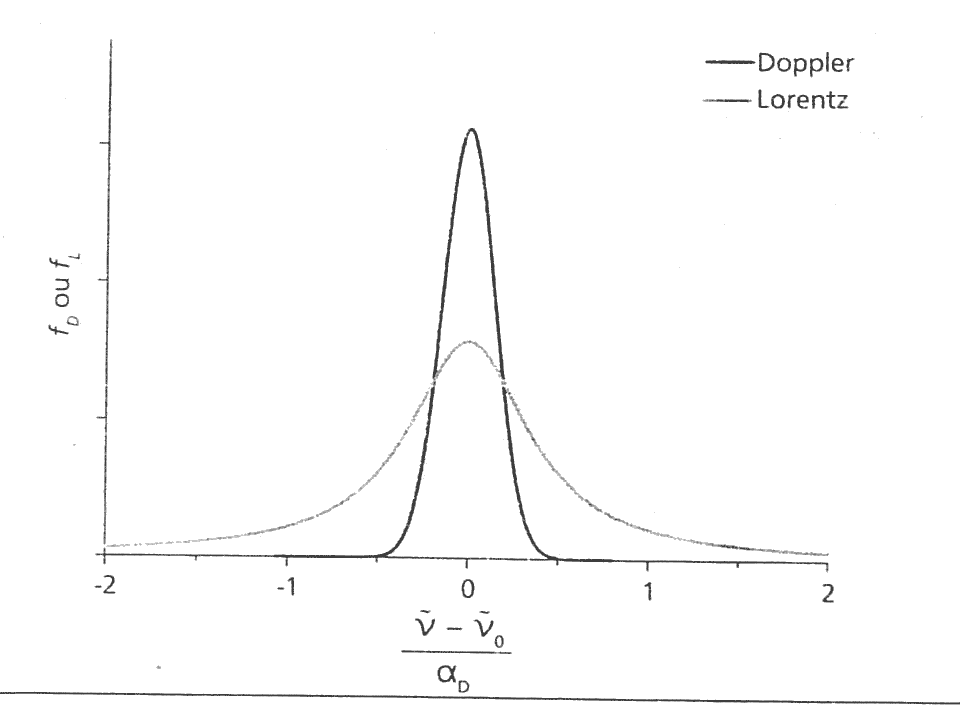 \[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]
\[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]
- \(k_a(\nu)\) é definido para cada ponto do espectro (cm²/g).
Seção de Choque e Coeficiente de Atenuação linear
- Seção de Choque: a área EFETIVA de absorção em um elemento do gas: \[ \sigma_a(\nu,z) = k_a(\nu)\rho(z)dA dz,\]
Onde \(\rho(z)\) é a densidade de massa do gás (g/cm³) no ponto \(z\).
- O Coeficiente de Absorção (ou atenuação ou extinção) é dado por: \[\beta_a(\nu,z) = n(z)\sigma_z(\nu,z),\]
- onde \(n\) é a densidade numérica de moléculas (N/cm³)
Finalmente, a Profundidade Óptica é: \[\tau_z(\nu) = \int_0^\infty \beta_a(\nu) dz.\]
Profundidade Óptica, Coeficiente de Atenuação e Seção de Choque
- Lembre da Lei de Beer - Redução da intensidade radiante: \[ I(z) = I_0 e^{-\tau_a} = I_0 e^{-\beta_a z} = I_0 e^{-\sigma_a n z} = I_0 e^{-k_a \rho z}, \] para uma atmosfera constante (tipo dentro de um tubo de laboratório).
- \(z\) - comprimento do tubo (cm)
- \(beta_a\) - coeficiente de absorção (1/cm)
- \(\rho\) - densidade de massa do gás (g/cm³)
- \(k_a\) - coficiente de absorção de massa (cm²/g)
On usando integrais: \[ I(z) = I_0 e^{-\int_0^z k_a \rho dz}.\]
Note que \(k_a=k_a(p,T)\), e \(\rho=\rho(p,T)\) e por sua vez \(p=p(z)\) e \(T=T(z)\), dependência na altitude \(z\).
Exercício
- 5.1: Ao nível do mar e à temperatura igual a 0C, a largura da linha \(\alpha\) do perfil de Lorentz corresponde a 0,08/cm para uma linha de absorção de um determinado gás. A 500mbar e à temperatura T=-30C, a mesma linha espectral será mais larga ou mais estreita? O que isso implica na absorção e na profundidade óptica?
Espalhamento
- A MAIORIA da radiação que vemos não vem diretamente da fonte! Ela é ESPALHADA.
- Espalhamento, mudanção da direção e indensidade da luz, sem alterar seu comprimento de onda.
- Ex. A folha espalha o verde mais do que o vermelho. (ete é absorvido)
- Causado por: moléculas, partículas, gotículas e gelo (núvens)
- Ex. Azul do ceu, Arco-íres, nuvem branca, halos...
Padrão de Espalhamento
- Dois tipos:
- Espalhamento Rayleigh (reili ou raili), quando a partícula é muito pequena.
Espalhamento Mie (mi), bem mais complexo, quando a partícula é grande.
- Raio incidente: ângulo 0.
- Feixe espalhado: para vários ângulos \(\Theta\)
- Dado por uma distribuição de ângulos: \(P(\Theta)\).
Forma do espalhamento depende da relação entre o comprimento de onda incidente \(\lambda\) e o tamanho da partícula \(R_p\).
- Para \(R_p << \lambda\) temos um espalhamento esférico (uniforme para todas as direções)
Para \(R_p >> \lambda\) temos um espalhamento linear (quase toda a energia segue para frente, com uma pequena parcela que volta.
Padrão de Espalhamento - Exemplo
Espalhamento Rayleigh
- Calculado em 1871 - Lord Rayleigh.
- Partículas bem pequenas: \(R< 0,1\lambda\)
- Partícula é vista como um dipolo elétrico.
- Solução para Profundidade Óptica: \[ \tau_R(\lambda) \approx \frac{1}{\lambda^4},\]
- Quando menor o comprimento de onda, MUITO MAIS é espalhada!
- O céu é azul
- Azul (\(\lambda \approx 0,425\mu m\)), Vermelho (\(\lambda \approx 0,650\mu\)).
- Azul espalha 5,5 vezes mais que o Vermelho.
- O Violeta espalha ainda mais, mas não tem tanto violeta quanto azul.
- Quando o sol se põe é Vermelho
- Porque o Azul já espalhou!
Espalhamento Mie
- Calculado por Gustav Mie (1908), para partículas esféricas de tamanho arbitrário.
- Serve para aerosol, gotas de chuvas, etc... visível até micro ondas e mais...
- Fenômenos:
- Reflexão (especular) na superfície da partícula.
- Refração (mudança de ângulo da trajetória) no movimento dentro da partícula.
- Difração (mudança de raio retilíneo para onda difratada em todas as direções)
Índide de Refração
- Refração: a mudança de ângulo de um raio de luz ao atravessar uma fronteira entre dois materiais:
Índide de Refração
Parametrizado pelo Índide de Refração: 
- \(\theta_1\) e \(\theta_2\) são os ângulos normais.
- \(n_1\) e \(n_2\) são os índices de refração de cada meio (ar e vidro, por exemplo)
Lei de Snell: \[n_1 \sin\theta1 = n_2\sin\theta2.\]
Ex: \(n_{ar}=1,000293\), \(n_{vidro}=1,52\). Para os dois casos: \(theta_{ar}=0\) e 30 graus, temos: \(\sin\theta_{vidro}=n_{ar}/n_{vidro}\sin\theta_{ar}\). \[\theta_{ar}=0\rightarrow \theta_{vidro}=0.\] \[\theta_{ar}=0\rightarrow \arcsin(1,000293/1,52)\sin30=\arcsin(0,329)=19.21^\circ.\]
Índice de Refração
- A refração explica o arco-ires (ou prisma):

Índice de Refração
- No arco-ires, onde estão os "prismas"?

Índice de Refração (explicação)
- A explicação: a luz muda de velocidade
- A luz é uma onda (do campo Eletromagnético)
- As cargas do meio material oscilam juntamente com o campo EM.
- Pela oscilação, as cargas emitem radiação EM com mesma frequencia, mas fase diferente.
- A onda resultante (onda original+onda emitida) tem a mesma frequencia mas comprimento de onda menor.
- Isso causa uma mudança de ângulo:
Índice de Refração (explicação)
- Redução de \(\lambda\) é o mesmo que redução de \(v\).
Índide de Refração e Absorção
Em uma onda, o índice de refração aje no "número de onda" \(k\): \[ \cos(kx - \nu t)\rightarrow \cos(nkx - \nu t).\]
Como \(v=\lambda \nu = \frac{1}{nk}\nu = \frac{v_0}{n}.\)
O processo de Absorção tembém é descrito usando "índice de refração", mas esse sendo "complexo".
Números complexos: \(z=a+bi\), onde \(i=\sqrt{-1}\).
Obedecem a fórmula de Gauss: \[ e^{ia} = \cos{a}+i\sin{a}.\]
Uma onde pode é a parte REAL de uma exponencial imaginária: \[ \cos{(kx-\nu t)} = \Re{e^{i(kx-\nu t)}}. \]
Quando \(n\) é complexo: \(n = n_r + i n_i\) temos: \[ \Re{e^{i((n_r+in_i)kx-\nu t)}} = e^{-2\pi n_i kx}\cos{(kx-\nu t)}.\]
Índide de Refração e Absorção (cont)
Na verdade, \(n_i\) é diretamente relacionado com o coeficiente de extinção \(\beta\):
Lembrando que a Energia de uma onda é o Quadrado da amplitude, o decaimento exponencial fica: \[ (e^{-2\pi n_i kx})^2 = e^{-\beta x},\qquad \beta=4\pi n_ik\]
Núvens
- Núvens: Cobrem 40% a 60% da superfície da Terra.
- Refletem, Absorvem e Transmitem radiação solar (visível)
- R,A,T e Emitem radiação terrestre (IV térmico)
- Baixas: refletem radiação solar (para cima). Esfria o solo.
- Altas: absorvem e reemitem (parte para baixo) o IV Térmico. Esquenta o solo.
- Gotas de água: grandes, esféricas, \(n\) real:
- Espalhamento independente de \(\lambda\), eficiente espalhador, não absorve visível.
- Modelos:
Núvens - Profundidade Óptica (Visível)
- Em uma núvem - Conteúdo de água líquida (w): \[ w = \frac{4\pi}{3}\rho\int r^3 n_g(r) dr,\]
- \(n_g(r)\) a distribuição de número de gotas com certo raio \(r\) em uma dado volume de ar.
- \(\rho\) - densidade da água líquida.
- \(w\) é em massa (g ou kg) naquele dado volume de ar.
- Num caminho vertical (de baixo para cima) - conteúdo de água líquida (LWP): \[ LWP = \int_{solo}^{topo} w(z) dz.\]
- Ráio efetivo (volume sobre area): \[ r_{eff} = \frac{\int r^3 n_g(r)dr}{\int r^2 n_g(r)dr}.\]
Núvens - Profundidade Óptica (Visível)
- Pode-se mostrar que a Profundidade Óptica de uma núvem \(\tau_{nuvem}\) é dado por: \[ \tau_{nuvem} = \frac{3}{2\rho}\frac{LWP}{r_{eff}}.\]
- Aumenta com a quantidade de água e diminue com o aumento do raio efetivo.
Núvens - Profundidade Óptica (IV)
- No IV, a água passa a absorver radiação EM (\(n\) complexo, \(\beta\ne 0\)).
- Em média: Refletem 74%, Absorvem 10%, Transmitem 16%.
- Nas JANELAS atmosféricas (8,5µm a 12,5µm) - Obedeçem o espalhamento Mie.
- Sem espalhamento, a Emissividade é aproximada por: \[\epsilon(\lambda) = 1-e^{-\beta(\lambda)\Delta z}\] com \(\beta\) dado por \[\beta = \frac{3a_0}{4\rho}\frac{w}{r_{eff}}.\]
- Aumento com a espessura (quatidade de água por volume) e diminue com o raio efetivo.
Exercício 5.6
Considere uma núvem de \(h=1\)km de espessura, com profundidade óptica igual à 1 \(\tau=1\). Assumindo que ela contenha 1000 gotas por unidade de volume (digamos \(m^3\)), estime:
- O tamanho efetivo de cada gotícula (\(r_{eff}\)).
- Se o caminho óptico fosse aumentade do 10%, de quantos % variaria a transmitância?
Note que, \(\tau\) (profundidade óptica) é dada, para núvens, por: \[\tau=\frac{3}{2\rho}\frac{LWP}{r_{eff}} = 1\].
O LWP é dado por: \[LWP = \int_0^{1km} w dz,\] e \[w=\frac{4\pi}{3}\rho\int_0^{\infty}r'^3 N(r')dr'\].
Vamos então começar por \(w\).
Delta de Dirac
- \(N(r)\) é o número de gotículas de raio \(r\), por unidade de volume.
- No nosso caso ela é uma distribuição especial: todas as gotículas tem o mesmo \(r_0\) constante, e há 1000 delas por unidade de volume.
- Para representar esta distribuição, usamos a "função" Delta de Dirac, ou função impulso.
- \(\delta(x) = 0\), se \(x\ne0\), e
- \(\delta(x) = \infty\), se \(x=0\), e (o mais importante)
- \(\int_{-\infty}^{\infty} \delta(x)dx = 1\), e isso implica que:
- \(\int_{-\infty}^{\infty} f(x)\delta(x) dx = f(0),\) e também implica que:
- \(\int_{-\infty}^{\infty} f(x)\delta(x-x_0) dx = f(x_0).\) O mesmo é:
- \(\int_{x_0-\epsilon}^{x_0+\epsilon} f(x)\delta(x-x_0) dx = f(x_0),\) e também implica que:
Delta de Dirac
N e W
Assim: \[ N(r) = 1000 \delta(r-r_0),\] onde \(r_0\) é o valor do raio das gotículas.
Agora podemos calcular \(w\):
\[ w=\frac{4\pi}{3}\rho\int_0^{\infty} r^3N(r)dr = \] \[ w=\frac{4\pi}{3}\rho\int_0^{\infty} r^3 1000 \delta(r-r_0)dr = \]
Finalmente: \[ w=\frac{4\pi}{3}\rho r_0^3 1000.\]
LWP e reff.
Para calcular LWP, fazemos a integral na vertical. Aqui \(w\) não varia com a altitude (isso poderia ser o case se \(N\) dependensse de \(z\)).
\[LWP = \int_0^{h} w dz = \frac{4\pi}{3}\rho r_0^3 1000 h.\]
O Raio efetivo é dado pela fórluma:
\[r_{eff} = \frac{\int r^3 N dr}{\int r^2 N dr} = \] \[ \frac{\int r^3 1000\delta(r-r_0)dr}{\int r^2 1000\delta(r-r_0)dr} = \] \[ \frac{1000 r_0^3}{1000 r_0^2} = r_0.\]
Logo \(r_{eff}=r_0\).
LWP, \(\tau\) e \(r_0\)
A profundidade óptica \(\tau\) é dada por:
\[\tau = \frac{3}{2\rho}\frac{LWP}{r_{eff}} = \] \[\tau = \frac{3}{2\rho}\frac{\frac{4\pi}{3}\rho r_0^3 1000 h}{r_0} = \] \[\tau = 2\pi r_0^2 1000 h.\]
Finalmente, o raio efetivo é dado por:
\[r_{0} = \sqrt(\tau/(2\pi 1000 h)) = 0.0004m = 0.4mm.\]
Mudança no Caminho óptico:
Se aumentarmos em 10% o caminho óptico - o percurso da luz - Quanto muda a transmitância? Lembre que \(T=e^{-\tau}\). Expresse em porcentagem.
Assim:
\[ T=e^{-\tau} = e^{-\tau_0*1.1}.\]
Mudança percentual
- A mundaça fracional (percentual) de uma grandeza é:
\[ \Delta \% = \frac{T-T_0}{T_0} = \frac{T}{T_0}-1. \]
\[ \Delta \% = \frac{e^{-1.1\tau_0}}{e^{-\tau_0}} -1 = e^{-1.1\tau_0+\tau_0} -1= \] \[ \Delta \% = e^{-0.1\tau_0} -1 = e^{-0.1} -1= 0.905-1 = -0.095 = -9.5\%.\]
Problema 5.4
- O índice de refração \(n\) no ar depende aproximadamente do número de moléculas por centímetro cúbico. E pode ser aproximado por:
\[ (n-1) = cN\],
onde \(c\) é uma constante a determinar, e \(N\) é o número de moléculas por volume.
Na superfície, \(n=1,000292\).
Se em \(z=0\), \(N_0=25.5\times 10^{18}\), e \(N_{10km}=8.6\times 10^{18}\), calcule \(n\) a 10km.
Regra de 3:
\[ (n_0-1) = c N_0\] \[ (n_{10km}-1) = c N_{10}\]
\[ (n_{10km}-1) = (n_0-1)*N_{10}/N_{1} = 0.000292 \frac{8.6}{25.5}\] \[(n_{10km}-1) = 0.3373(n_0-1) = 0.000985,\] \[n_{10km}= 1.000985.\]
Equação da Transferência Radiativa
- A ETR é a equação fundamental para o estudo da propagação da radiação.
- Em uma região do espaço:
- A Radiação que sai
- menos a Radiação que entra
- é o saldo de radiação
- Este Saldo é dado pela soma de todos os processos radiativos:
- absorção
- emissão
- remoção por espalhamento
- adição por espalhamento (de outroas fontes)
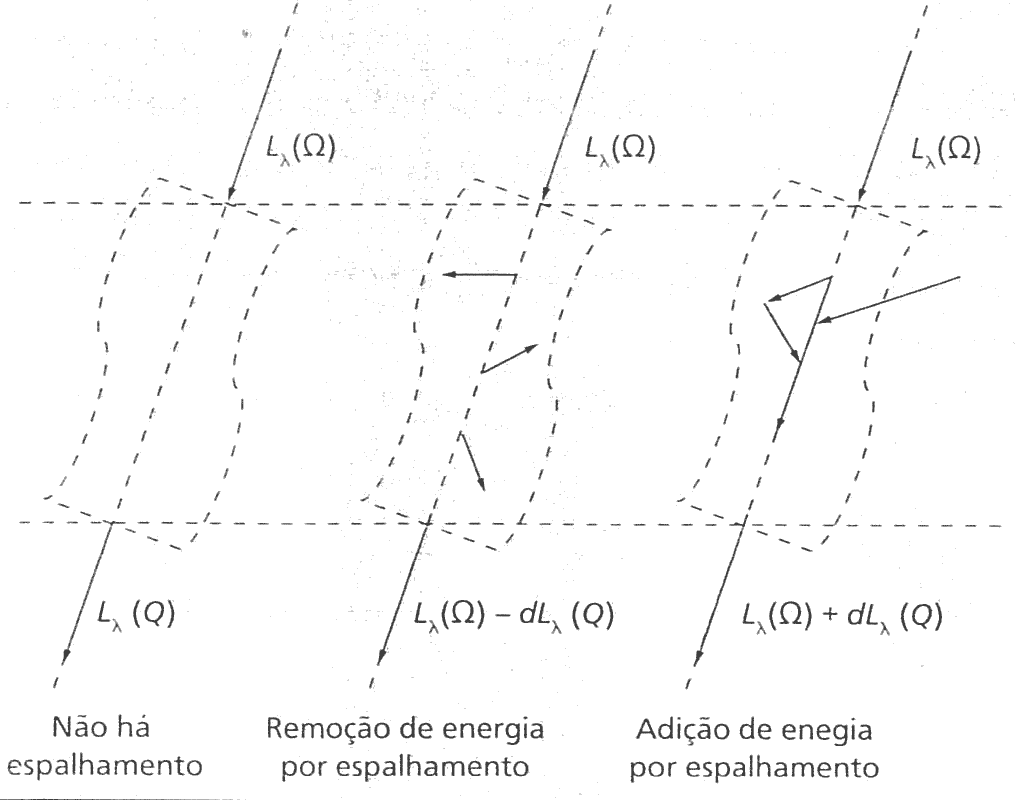
Lei de Beer
- Vamos começar por algo simples: \(T = e^{-\tau}\), a Lei de Beer.
- Considere um feixe de radiância espectral \(L_\lambda\)
- Orientado na direção \(\Omega = (\theta, \phi)\).
- lembre-se: W/m²/sr/\(\mu\)m.
- Esse feixe atravessa uma região do espaço:
- Uma região infinitesimal de largura \(ds\) na posição \(s\) (vamos considerar área constante).
- Este volume contém gotículas/partículas (espalhamento), e moléculas (absorpção).
- O feixe então sofre absorção e espalhamento - aqui estamos considerando apenas os aspéctos de atenuação.
Lei de Beer
Lei de Beer - coeficientes
- O coeficiente linear de atenuação resume todos os processos físicos de atenuaçào.
- Pode-se dividir em duas partes: absorção e espalhamento:
\[ \beta_\lambda(s) = \beta_{a\lambda} + \beta_{e\lambda}, \]
\[ \beta_\lambda(s) = k_\lambda(s)\rho(s) = \sigma_\lambda(s) N(s),\]
- \(k_\lambda(s)\) (m²/kg) é o coef. mássico de atenuação, \(rho\) é a densidade (kg/m³).
- \(\sigma_\lambda(s)\) (m²) é a seção de choque, e \(N\) é a densidade de partículas (#/m³).
Lei de Beer - Integral
- A equação diferencial da conservação da energia pode ser integrada (equação diferencial linear de primeira ordem).
\[ dL_\lambda(\Omega,s) = -L_\lambda(\Omega,s)\beta_\lambda(s)ds \rightarrow \frac{dL_\lambda(\Omega,s)}{L_\lambda(\Omega,s)} = -\beta_\lambda(s)ds,\] \[ \int_{L(s_1)}^{L(s_2)}\frac{dL_\lambda(\Omega,s)}{L_\lambda(\Omega,s)} = -\int_{s_1}^{s_2}\beta_\lambda(s)ds,\] \[ \ln L_\lambda(\Omega,s_2) - \ln L_\lambda(\Omega,s_1) = -\int_{s_1}^{s_2}\beta_\lambda(s)ds,\] \[ \ln\left(\frac{L_\lambda(\Omega,s_2)}{L_\lambda(\Omega,s_1)}\right) = -\int_{s_1}^{s_2}\beta_\lambda(s)ds \rightarrow L_\lambda(\Omega,s_2) = L_\lambda(\Omega,s_1) e^{-\int_{s_1}^{s_2}\beta_\lambda(s)ds}.\]
Definindo \(\tau = \int_{s_1}^{s_2}\beta_\lambda(s)ds\), temos a Lei de Beer: \(L=L_0e^{-\tau}\).
- NOTE: Como ela \(\tau\) é uma integral, ela é aditiva: se você junta duas porções com espessura óptica \(\tau_1\) e \(\tau_2\), a resultante será: \(\tau=\tau_1+\tau_2\).
Exercício:
- 6.1 Um sinalizador emite um feixe direto de radiação monocromática (\(\lambda=0,55\mu\)m) de potência 1000W/m² a ser recebido por um alvo postado a uma distância arbitrária de um caminho óptico cujo coeficiente linear de atenuação é \(\beta\)/m. Um sensor postado a 50m do sinalizador mede a irradiância de 82,1W/m². Sabendo que esse sensor não mede irradiâncias inferiores a 0,1W/m², determine a distância máxima na qual pode ser colocado o sensor para que ele detecte a presença do sinalizador.
Equação da Transferência Radiativa
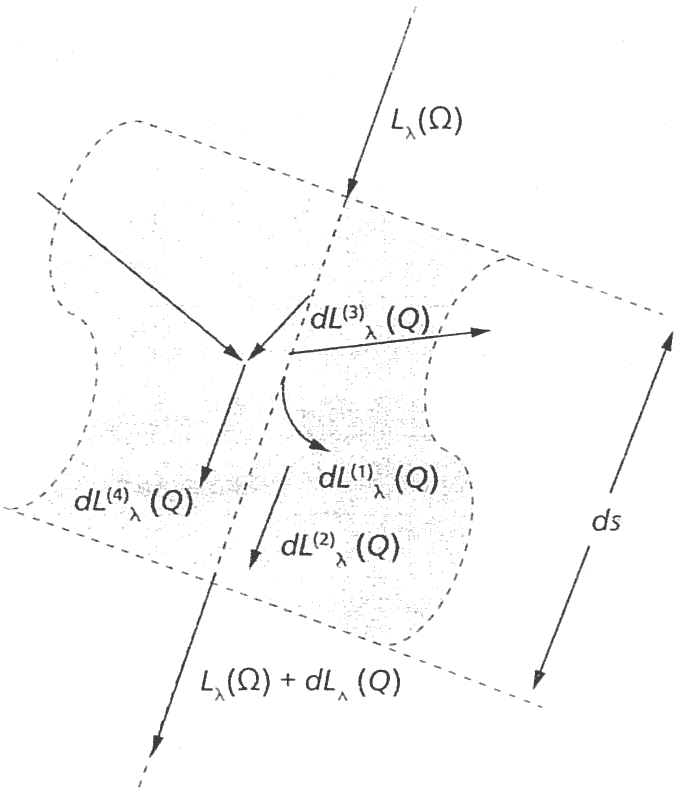
- Quando um feixe \(L_\lambda(\Omega)\) atravessa a matéria pode ocorrer:
- Absorção - menos fótons no feixe-> Lei de Beer. (meio molecular absorve energia radiante - aumento da energia interna do meio)
- Emissão - mais fótons no feixe. (meio molecular emite energia rafiante - diminuição da energia interna do meio)
- Espalhamento de dentro de \(L\) para fora - menos fótons no feixe. (partículas espalham energia radiante para fora do feixe - maior energia para o meio)
- Espalhamento de fora de \(L\) para dentro - mais fótons no feixe. (partículas espalham energia de fora do feixe para dentro do feixe - aumento da energia interna do meio).
- Assim: \(dL = -dL^1 + dL^2 - dL^3 + dL^4\):
- Quando \(dL<0\) energia fica dentro do meio - esquenta!
- Quando \(dL>0\) energia sai do meio - esfria!
Equação da Transferência Radiativa
- Meio material onde há apenas absorção e emissão eletrônicas/moleculares.
- Sem nenhum espalhamento (sem partículas de tamanho considerável, ignora-se Rayleigh).
- Assim:
\[dL = -dL^{abs} + dL^{emis}.\]
- Já vimos o que é \(dL^{abs}\): \[ dL^{abs}(s) = L(s)\beta_{abs}(s) ds.\]
- O que seria a emissão \(dL^{emis}\)? Lei de Kirchoff:
- Para um corpo-negro: A Emissividade é igual ao coeficiente de absorção: \[\epsilon_\lambda = a_\lambda = \frac{dL^{abs}{}_\lambda}{L_\lambda} = \beta_{abs}{}_\lambda ds.\]
- A emissividade é, para corpo-negro de temperatura \(T\) (lei de Plank): \[\epsilon_\lambda = \frac{dL^{emis}{}_\lambda}{B(\lambda,T)}.\]
- Assim: \[dL^{emis} = \epsilon_\lambda B(\lambda,T) = \beta_{abs}{}_\lambda B(\lambda,T) ds.\]
- Juntando ambas as contribuições, temos:
\[ dL = \beta_{abs}(-L + B(T)) ds, \] ou \[ dL_\lambda(\Omega,s) = \beta_{abs}{}_\lambda(s)(-L_\lambda(\Omega,s) + B(\lambda,T(s))) ds, \] ou \[ \frac{dL_\lambda(\Omega,s)}{\beta_{abs}{}_\lambda(s) ds)} = -L_\lambda(\Omega,s) + B_\lambda(T(s)).\]
- Essa é a forma diferencial da ETR sem espalhamento e é chamada de
- Boa aproximação:
- Nas regiões espectrais onde não ocorre emissão/absorção (Janelas)
- Ex. visível: Regiões entre 0,35\(\mu\)m e 0,40\(\mu\)m.
\[ dL = -dL^{fora} + dL^{dentro},\]
- \(dL^{fora}\) - espalhamento da radiação incidente seguindo \(\Omega\) para outras direções.
- \(dL^{dentro}\) - espalhamento de outras direções para a direção de \(\Omega\).
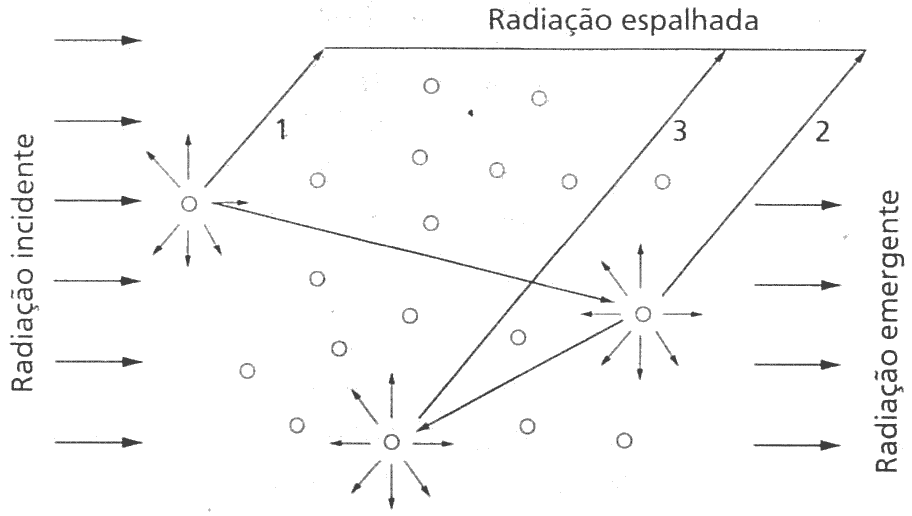
- O espalhamento pode ser múltiplo: fóton bate em mais de uma partícula.
- Probabilidade disto aumenta com \(\tau\).
Redução/adição de radiação por espalhamento
Espalhamento múltiplo
A atenuação por espalhamento: \[ dL^{fora}(s) = L(s) \beta_{esp}(s)ds.\]
A adição por espalhamento, vem da radiação difusa (espalhada de outro lugar): \[ dL^{dentro}(\Omega, s) = J(\Omega,s) \beta_{esp}(s)ds.\]
\(J(\Omega)\) ou \(J_\lambda(\Omega, s)\), é a função fonte por espalhamento:
\[ J(\Omega)=\frac{1}{4\pi}\int_{4\pi}L(\Omega')p(\Omega',\Omega)d\Omega',\] Onde \(L(\Omega')\) é a radiância disponível vindo de outras direções, e \(p(\Omega',\Omega)\) é a função de fase.
Assim: \[ \frac{dL_\lambda(\Omega,s)}{\beta_{esp}{}_\lambda(s)ds} = -L_\lambda(\Omega,s)+J_\lambda(\Omega,s).\]
Equação da Transferência Radiativa - completa
- Juntando todos os quatro fenômenos temos:
- Todas as variáveis podem depender de \(\lambda\), \(s\) e \(\Omega\):
\[ dL(\Omega) = (-L\beta_{abs} - L\beta_{esp} + B(T)\beta_{abs} + J(\Omega)\beta_{esp}) ds.\]
- Definindo o coeficiente de atenuação total \(\beta=\beta_{abs}+\beta_{esp}\).
- Definindo o Albedo de espalhamento único (single scattering albedo): \(\omega_0 = \beta_{esp}/\beta\), temos que
\[ \beta_{esp}(s) = \omega_0(s)\beta(s),\] \[ \beta_{abs}(s) = (1-\omega_0(s))\beta(s).\]
Equação da Transferência Radiativa - completa
- Trocando na expressão da ETR, temos:
\[ dL = -L\beta ds + B(T(s))(1-\omega_0(s))\beta(s) ds + J(\Omega,s)\omega_0(s)\beta(s) ds,\]
\[ \frac{dL_\lambda(\Omega,s)}{\beta_\lambda(s)ds} = -L_\lambda(\Omega,s) + (1-\omega_0(\lambda,s))B(\lambda,T(s)) + \omega_0(\lambda,s)J(\lambda,\Omega,s).\]
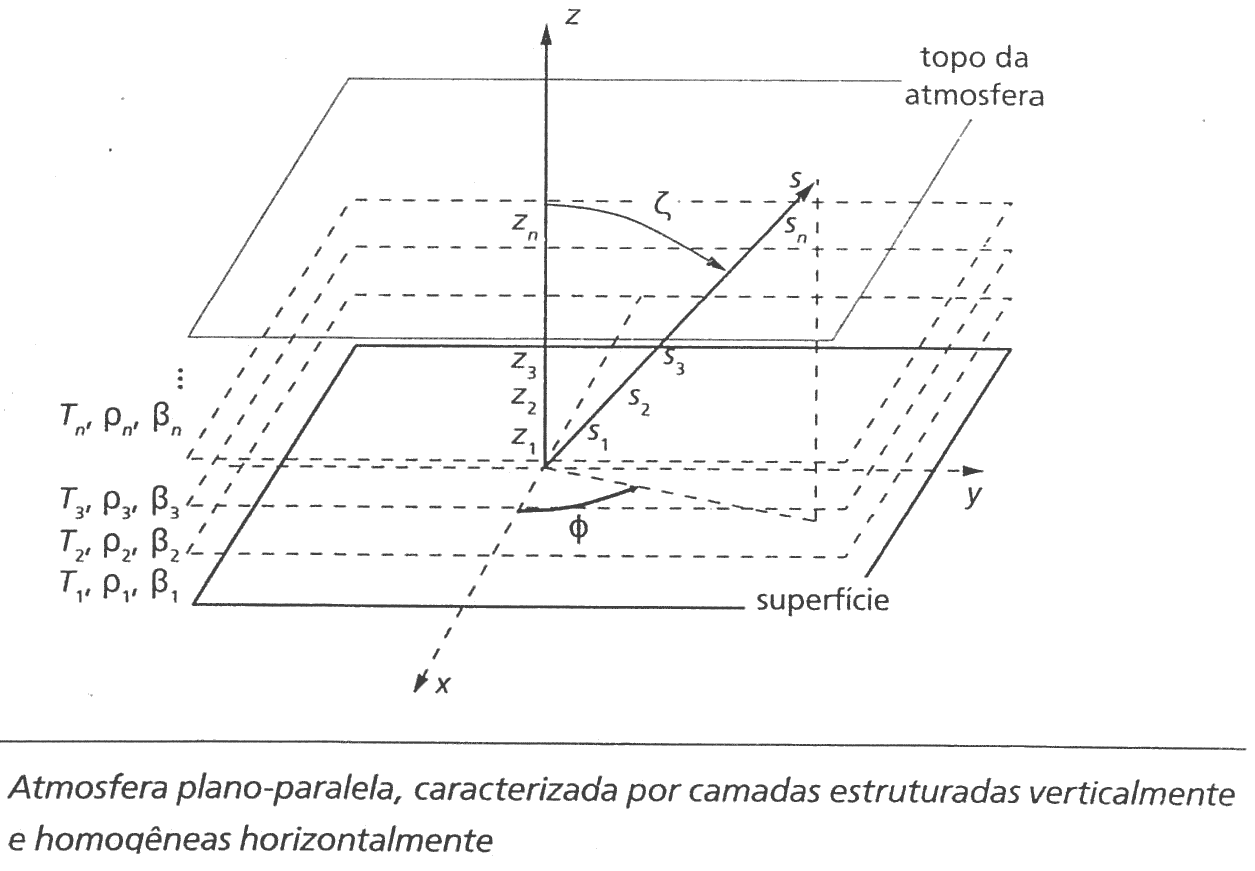
Aproximação de atmosfera plano-paralela ("Terra Plana")
Aproximação de atmosfera plano-paralela ("Terra Plana")
- Coordenadas Locais: ângulo zenital (\(\zeta\), do topo para baixo) e ângulo azimutal (\(\phi\), do Norte para Leste).
- Onde define-se: \(\mu=\cos{\zeta}\) (varia de 1 (zenit) ao 0 (horizonte)).
- Positivo (+) ascendente.
- Negativo (-) descendente.
- Coordenada do caminho óptico é a própria vertical \(z\) - tudo é função de \(z\).
- \(z\) é zero no nível do mar,
- Relação entre \(z\) e o caminho óptico: \(z=s\cos\zeta\) ou \(z=\mu s\).
- A atmosfera é homogênea (constante) na horizontal (\(x\),\(y\)), logo uma grandeza é a mesma estndo exatamente sobre as nossa cabeças ou em um outro ângulo, o que importa é a altitude.
Aproximação de atmosfera plano-paralela ("Terra Plana")
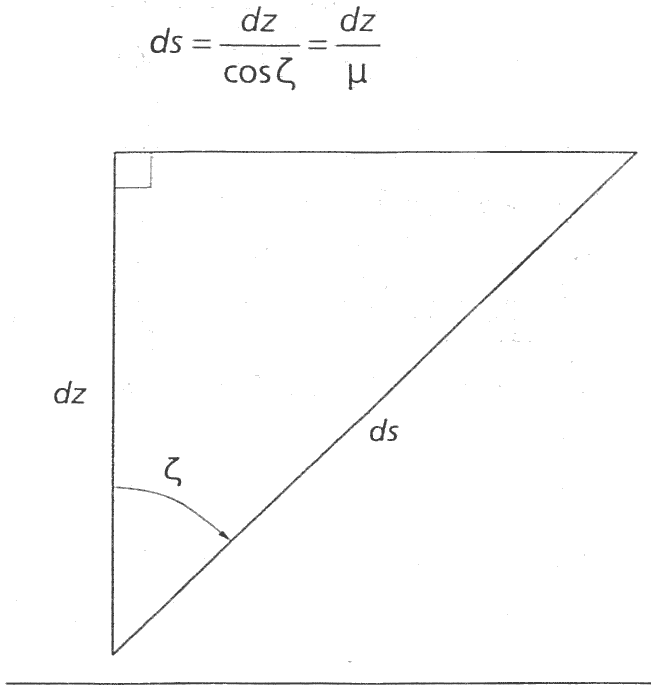
- Como a atmosfera muda com \(z\), há a relação entre \(ds\) e \(dz\):
Integral da ETR na atmosfera Plano-Paralela
\[ \frac{dL_\lambda(\Omega,s)}{\beta_\lambda(s)ds} = -L_\lambda(\Omega,s) + (1-\omega_0(\lambda,s))B(\lambda,T(s)) + \omega_0(\lambda,s)J(\lambda,\Omega,s).\]
- Vamos trocar o "abstrato" \(\Omega\) pelos "concretos" \(\zeta\) e \(\phi\).
- A profundidade óptica é dada por \(\frac{d\tau(z)}{dz}=-\beta(z)\).
- O efeito do ângulo de visada \(\zeta\) entra na definição de \(ds\), assim temos:
\[ \frac{\mu dL_\lambda(z,\mu,\phi)}{\beta_\lambda(z)dz} = -L_\lambda(z,\mu,\phi) + (1-\omega_0(z))B(T(z)) + \omega_0(z)J(z,\mu,\phi).\]
- Como função de \(\tau\) é uma E.D.O 1a ordem - que tem solução geral.
Integral da Equação da Transferência Radiativa
\[\frac{1}{\beta}\frac{dL}{ds}=-L+(1-\omega_0)B+\omega_0 J,\] lembrando que \(\beta=\beta_{abs}+\beta_{esp}\), \(\omega_0=\beta_{esp}/\beta\), \(B\) é função de Plank e \(J\) é função fonte de espalhamento.
- É uma equação de primeira ordem. Tem solução geral.
Muitos livros fazem a seguinte transformação: \[ \beta ds = d\tau \quad\rightarrow\quad \frac{1}{\beta}\frac{dL}{ds} = \frac{dL}{d\tau},\] onde \(\tau=0\) é em \(s=0\). Isso permite uma integral formal: \[ \frac{dL}{d\tau}=F(\tau) \quad\rightarrow\quad L(\tau)=L(\tau_0)e^{\int_{\tau_0}^{\tau}F(\tau')d\tau'},\] onde toda a complexidade está escondida na relação implicita entre \(\tau\) e \(z\).
Faremos aqui de forma mais explicita.
Integral da ETR Térmica
- Por simplicidade faremos apenas a parte Térmica, sem espalhamento (\(\omega_0=0\)).
- Depois basta trocar \(B\) por \((1-\omega_0)B+\omega_0 J\) e refazer as integrais.
- Vamos usar a aproximação plano-paralela. \[\frac{1}{\beta}\frac{dL}{ds} = -L+B.\]
- Na relação entre \(s\) e \(z\) teremos duas situações (aqui \(\cos\zeta=1\)):
- para cima (ascendente): \(z=s\).
- para baixo (descendente): \(z=z_{max}-s\).
- Usando a regra da cadeia: \[\frac{dL}{ds} = \frac{dL}{dz}\frac{dz}{ds},\] e \(dz/ds=+1\) se for acendente ou \(-1\) se for descendente. Logo: \[\frac{1}{\beta}\frac{dL}{dz} = \mp L + \pm B.\]
Integral da ETR Térmica - Ascendente
- Integral geral de \(L'+\beta L = \beta B\) usa o fator integrante: \[u(z) = \exp{\left(\int^z\beta(z')dz'\right)}.\]
- Note: Não importa o limite inferior, ele acaba sendo cancelado depois. Basta uma anti-derivada.
- Note 2: \(du/dz = \beta u\).
- Multiplicando \(u\) em ambos os lados, temos: \[uL' + \beta u L = \beta u B \quad\rightarrow\quad \frac{d(uL)}{dz} = \beta u B.\]
- Fazendo a integral ascendente (de \(z_0\) a \(z\)), e colocando \(u(z)\) explicitamente na direita:
\[\int d(uL) = \int_{z_0}^{z} \beta(z') u(z') B(z') dz' = \int_{z_0}^{z} \beta(z')B(z')e^{\int^{z'}\beta(z'')dz''}dz',\]
Integral da ETR Térmica - Ascendente
O lado esquerdo é o próprio \(uL\) nos limites: \[\int d(uL) = u(z)L(z) - u(z_0)L(z_0) = \int_{z_0}^{z} \beta(z')B(z')e^{\int^{z'}\beta(z'')dz''}dz'.\]
Passando para o lado direito \(u_0L_0\) e dividindo tudo por \(u(z)\): \[L(z) = \frac{u(z_0)}{u(z)}L(z_0) + \frac{1}{u(z)}\int_{z_0}^{z} \beta(z')B(z')e^{\int^{z'}\beta(z'')dz''}dz'.\]
- Note: \[\frac{u(z_0)}{u(z)}=\frac{e^{\int^{z_0}\beta dz'}}{e^{\int^z\beta dz'}}=
e^{\int^{z_0}\beta dz'}e^{-\int^z\beta dz'}=e^{-\int_{z_0}^z\beta dz'}. \]
Que é o termo de atenuaão da lei de Beer. (Por isso o limite inferior não importava!)
Integral da ETR Térmica - Ascendente
Assim temos: \[L(z) = L(z_0)e^{-\int_{z_0}^z\beta dz'} + e^{-\int^z\beta dz''}\int_{z_0}^{z} \beta(z')B(z')e^{\int^{z'}\beta(z'')dz''}dz'.\]
Colocando a exponencial de fora para dentro da integral, temos:
\[L(z) = \underbrace{L(z_0)}_{Emissão da superfície}\underbrace{e^{-\int_{z_0}^z\beta dz'}}_{Atenuação atmosférica Lei de Beer} + \int_{z_0}^{z} \underbrace{\beta(z')B(z')}_{Emissão na altitude z'}\underbrace{e^{-\int_{z'}^z\beta(z'')dz''}}_{Atenuação de $z'$ até $z$}dz'.\]
Integral da ETR Térmica - Ascendente
- Simplificação: quand \(\beta\) e \(B\) são constantes (dentro de um laboratório, por exemplo), e que \(z_0=0\):
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')dz''} dz'= \] \[L(z) = L_0e^{-\beta z} + \beta B(T) \int_{0}^{z} e^{-\beta (z-z')} dz'. \]
- Trocando \(x=z-z' \rightarrow dx=-dz'\), e os limites \(z'=0\rightarrow x=z,\quad z'=z\rightarrow x=0\) temos: \[\int_{z}^{0} e^{-\beta x} (-dx) = \frac{1}{\beta} e^{-\beta x}|_{z}^{0} = \frac{1}{\beta}(1-e^{-\beta z}).\]
Assim: \[L(z) = L_0e^{-\beta z} + \beta B(T) \frac{1}{\beta}(1-e^{-\beta z}) = \] \[L(z) = L_0e^{-\beta z} + B(T) (1-e^{-\beta z}). \]
Integral da ETR Térmica - Ascendente
- Para outro ângulo zenital \(\zeta\) basta trocar:
\[ ds=dz \rightarrow ds=\frac{dz}{\cos\zeta}=\sec\zeta dz, \] usando a secante nas expressões, ou seja:
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta \sec\zeta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')\sec\zeta dz''}\sec\zeta dz.\]
- Para o caso particular de \(\beta\) e \(B\) constantes, temos:
\[L(z) = L_0e^{-\beta\sec\zeta z} + B(T)(1-e^{-\beta\sec\zeta z}).\]
- Lembre que em geral \(\beta\) e \(T\) dependem de \(z\).
Integral da ETR - Exemplo
A Integral da ETR apenas com termos térmicos fica na forma:
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta \sec\zeta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')\sec\zeta dz''}\sec\zeta dz.\]
- Janela.
- Imagine uma janela atmosferica atmosférica (região do espéctro que a radiação eletromagnética atravessa a atmosfera sem alteração), na posição \(\lambda_0\).
- Considere a temperatura da superfície como sendo \(T_s=300K\).
- Assumindo que esta janela seja ideal (\(\beta=0\)), calcule a radiância sobe verticalmente (\(\zeta=0\)) e sai da atmosfera, chegando a um observador em órbita.
Integral da ETR - Exemplo
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta \sec\zeta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')\sec\zeta dz''}\sec\zeta dz.\]
- Perfil de temperatura.
- Imagine que agora existe um gás que é capaz de emitir/absorver nesse mesmo comprimento de onda, que contamina a atmosfera mas apenas em uma certa camada.
- Considere que este gás forma uma camada de espessura \(h\), ou seja \(h=z_2-z_1\), onde \(z_1\) é a base e \(z_2\) é o topo da camada de gás. Vamos considerar que \(z_1=10km\) e \(z_2=11km\).
- Utilizando um perfil de temperatura padrão, estime a temperatura da camada de gás \(T_g\).
Integral da ETR - Exemplo
- Efeito da Camada
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta \sec\zeta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')\sec\zeta dz''}\sec\zeta dz.\]
- Existe uma região espectral na atmosfera cujo gás Metano (CH4) é quase que o único gás presente na faixa centrada em 1305µm com largura de aproximadamente 5µm.
- Nesta faixa, o coeficiente de absorção \(\beta\) pode ser considerado como 0,1/km.
- Para um angulo de visada vertical \(\zeta=0\), calcule:
- A componente de absorção (lei de beer).
- A componente de emissão (reemissão).
- O valor total da radiância.
- Repita o cálculo para um ângulo azimutal \(\zeta\) de 45 graus e 90 graus.
Integral da ETR - Exemplo - Temperatura de Brilho
- Uma grandeza muito útil é a Temperatura de Brilho (Brightness Temperature):
- Se \(R_\lambda = B(T,\lambda)\) é a função de Plank, e \(R\) é a radiância emitida no comprimento de onda \(\lambda\) para uma certa temperatura \(T\), podemos inverter a relação:
- \(T_{b\lambda} = B^{-1}(R_\lambda,\lambda)\), onde \(T_{b\lambda}\) é a temperatura associada à radiância \(R_\lambda\), e \(B^{-1}\) é o inverso da função de Plank. Veja este pedaço de programa Matlab/Octave:
Integral da ETR - Exemplo - Temperatura de Brilho (matlab)
% Inputs:
% fr - vector of wavenumber (cm-1)
% rad - vector of radiances (mW/m2 per cm-1 per strad)
% bt - vector of brightness temperature (Kelvin)
fr = COLOQUE AQUI O VALOR DE fr (em cm¯¹)
% Se voce for calcular RAD, defina BT: %%%%%%%%%%%%%5
bt = COLOQUE AQUI O VALOR DA TEMPERATURA (rm K)
% Se voce for calcular BT, defina RAD: %%%%%%%%%%%%%5
rad = COLOQUE AQUI O VALOR DE rad (em mW/m²/cm¯¹/sr)
% Constants; values from NIST (CODATA98)
c = 2.99792458e+08; % speed of light 299 792 458 m s-1
h = 6.62606876e-34; % Planck constant 6.626 068 76 x 10-34 J s
k = 1.3806503e-23; % Boltzmann constant 1.380 6503 x 10-23 J K-1
% Compute radiation constants c1 and c2
c1 = 2*h*c*c * 1e+11; % Changed 1e+8 to 1e+11 to convert Watts to milliWatts
c2 = (h*c/k) * 100;
% return bt = c2 * fr / log(1 + c1 * fr^3 / rad)
% Se for calcular BT: %%%%%%%%%%%%%%
bt = c2 * fr ./ log(1 + c1 * (fr.^3) ./ rad);
% Se for calcular RAD: %%%%%%%%%%%%%%
rad = c1 * fr.^3 ./ (exp((c2 * fr) ./ bt) - 1);
Integral da ETR - Exemplo - Temperatura de Brilho (Python)
# Inputs:
# fr - vector of wavenumber (cm-1)
# rad - vector of radiances (mW/m2 per cm-1 per strad)
# bt - vector of brightness temperature (Kelvin)
import math
fr = COLOQUE AQUI O VALOR DE fr (em cm¯¹)
# Se voce for calcular RAD, defina BT: %%%%%%%%%%%%%5
bt = COLOQUE AQUI O VALOR DA TEMPERATURA (rm K)
# Se voce for calcular BT, defina RAD: %%%%%%%%%%%%%5
rad = COLOQUE AQUI O VALOR DE rad (em mW/m²/cm¯¹/sr)
# Constants; values from NIST (CODATA98)
c = 2.99792458e+08; # speed of light 299 792 458 m s-1
h = 6.62606876e-34; # Planck constant 6.626 068 76 x 10-34 J s
k = 1.3806503e-23; # Boltzmann constant 1.380 6503 x 10-23 J K-1
# Compute radiation constants c1 and c2
c1 = 2*h*c*c * 1e+11; # Changed 1e+8 to 1e+11 to convert Watts to milliWatts
c2 = (h*c/k) * 100;
# return bt = c2 * fr / log(1 + c1 * fr^3 / rad)
# Se for calcular BT: %%%%%%%%%%%%%%
bt = c2 * fr ./ math.log(1 + c1 * (fr^3) ./ rad);
# Se for calcular RAD: %%%%%%%%%%%%%%
rad = c1 * fr^3 / (math.exp((c2 * fr) / bt) - 1);
- Voce pode ir no site https://www.programiz.com/python-programming/online-compiler/ para testar o programa acima.
Integral da ETR - Exemplo - Temperatura de Brilho
\[L(z) = L(z_0)e^{-\int_{z_0}^z\beta \sec\zeta dz'} + \int_{z_0}^{z} \beta(z')B(z')e^{-\int_{z'}^z\beta(z'')\sec\zeta dz''}\sec\zeta dz.\]
- Considere radiação de número de onda \(k=1000/c\)m.
- Calcule o comprimento de onda \(\lambda\) (lembre-se \(\lambda = 10000/k\) em µm).
- Considere três casos com emissão de 0.5, 1 e 2 W/m²/sr/cm:
- Calcule o T associado a cada caso.
- No problema do Metano, assuma que a Temperatura de Brilho (Brightness temperature) da radiância que chega no observador no espaço seja de 240K. Estime \(\beta\) para o ângulo azimutal \(\zeta=0\).
Balanços Radiativos
- Em qualquer sistema, balanço: \(E^\text{abs} - E^\text{emit} = Q^\text{int}\).
- \(E\) (ou \(Q\)) aqui é o total de todas as formas de energia.
- No sistema da Terra, e no balanço radiativo normalmente dividimos as energias entre:
- \(E_c\): Ondas curtas: IR próximo, Vis, UV
- \(E_l\): Ondas longas: IR Termal
- Claro que existem outras formas de energia (calores sensíveis, latentes, mecânica, etc... mas não importam neste momento)
Balanços Radiativos
Assim temos: \[ Q^\text{int} = (E_c{}^{abs}-E_c{}^{emit})+(E_l{}^{abs}-E_l{}^{emit}) = Q_c{}^{tot}+Q_l{}^{tot},\] \[ Q^\text{int} = (E_c{}^{abs}+E_l{}^{abs}) - (E_c{}^{emit}+E_l{}^{emit}) = Q^{abs}-Q{}^{emit}.\]
No caso de balanço, \(Q^\text{int}=0\rightarrow Q^{abs}=Q^{emit}\). \[ Q_{abs} = Q_{emit} \rightarrow \int_0^\lambda Q_{abs}(\lambda)d\lambda = \int_0^\lambda Q_{emit}(\lambda)d\lambda.\]
Equilíbrio radiativo do Planeta - SEM ATMOSFERA
Equilíbrio radiativo do Planeta - SEM ATMOSFERA
Equilíbrio radiativo do Planeta - SEM ATMOSFERA
Assim: \[ E_0(1-r_s) \pi R^2 = \sigma T^4 4\pi R^2,\] ou \[ T = \left[\frac{(1-r_s)E_0}{4\sigma}\right]^{1/4}.\]
- No caso da Terra:
- \(E_0=1367\)W/m², \(r_s\approx 0,3\), assim:
- \(T\approx 255\)K. Gelado! Porque não tem atmosfera....
- Mesmo se o albedo fosse zero, T=279K, ainda frio.
- A atmosfera faz toda a diferença.
Ex. Calcule a temperatura da superfície da Lua.
- Modelo simplificado:
- Superfície: temperatura (\(T_s\)), reflectância (\(r_s\)), absorptância=emissividade, \(a_s=\epsilon_s=1\), vamos assumir corpo-negro.
- Atmosfera com uma única camada: temperatura (\(T_a\)), absorptância para ondas curtas \(a_c\) e longas \(a_l=\epsilon_l\).
- Irradiação no topo da atmosfera: \(E_0\).
Trocas de Energia
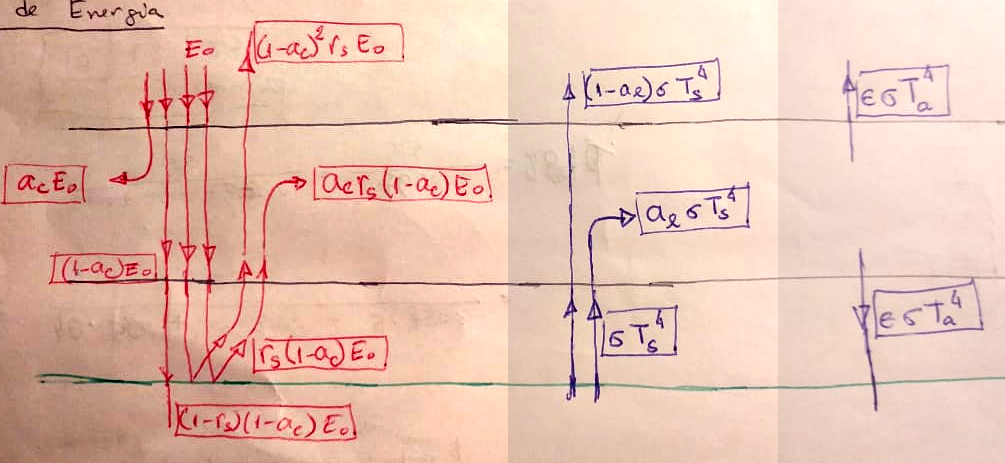
Balanco na Superfície: \[ (1-r_s)(1-a_c) E + a_l\sigma T_a^4 = \sigma T_s^4.\]
Trocas de Energia
Balanco na Atmosfera: \[ a_cE + a_cr_s(1-a_c)E + a_l\sigma T_s^4 = 2a_l \sigma T_a^4.\]
Trocas de Energia
Balanco no Topo da Atmosfera: \[ E = (1-a_c)^2r_sE + (1-a_l)\sigma T_s^4 + a_l\sigma T_a^4. \]
Trocas de Energia
\[ (1-r_s)(1-a_c) E + a_l\sigma T_a^4 = \sigma T_s^4.\] \[ a_cE + a_cr_s(1-a_c)E + a_l\sigma T_s^4 = 2a_l \sigma T_a^4.\] \[ E = (1-a_c)^2r_sE + (1-a_l)\sigma T_s^4 + a_l\sigma T_a^4. \]
As variáveis são \(T_a\) e \(T_s\) logo bastam duas equações (a 1a e a 2a). A 3a equação é automaticamente consistente, na verdade ela é a soma da 1a com a 2a!!
TENTE FAZER!
Resolução:
As equações são (reescrevendo o 1o termo da segunda equação):
\[ (1-r_s)(1-a_c)E + a_l\sigma T_a^4 = \textcolor{red}{\sigma T_s^4}, \]
\[ a_c(1+r_s(1-a_c))E + a_l\textcolor{red}{\sigma T_s^4} = 2 a_l\sigma T_a^4.\]
Substituindo a 1a na 2a equação, temos:
\[ \underbrace{a_c(1+r_s(1-a_c))E + a_l(1-r_s)(1-a_c)E}_{\text{mantem este como está}} + \underbrace{a_l^2\sigma T_a^4 = 2a_l \sigma T_a^4}_{=(2a_l-a^2)\sigma T_a^4 = a_l(2-a_l)\sigma T_a^4}, \]
assim:
\[ T_a^4 = \frac{\left\{ a_c\left(1+r_s(1-a_c)\right)+a_l(1-r_s)(1-a_c)\right\} E}{a_l(1-a_l)\sigma}.\]
Resolução:
E para \(T_s\):
\[ T_s^4 = \frac{1}{\sigma}\left( \textcolor{red}{(1-r_s)(1-a_c)}E + \frac{a_c(1+r_s(1-a_c))+a_l\textcolor{red}{(1-r_s)(1-a_c)}}{2-a_l}E\right) = \] \[ = \frac{\textcolor{green}{(2-a_l)}\textcolor{red}{(1-r_s)(1-a_c)} + a_l\textcolor{red}{(1-r_s)(1-a_c)} + a_c(1+r_s(1-a_c))}{\textcolor{green}{(2-a_l)}\sigma} E = \] \[ = \frac{2(1-r_s)(1-a_c)+a_c(1+r_s(1-a_c))}{(2-a_l)\sigma}E.\]
Casos Particulares
- Planeta com atmosfera transparente: \(a_c= a_l=0\):
Este caso é problemático, pois a nossa solução envolve divisões por \(a_l\). SEMPRE que se faz isso, assume-se que \(a_l\) não é zero explicitamente! Ao fazer \(a_l=0\) obtemos \(T_a = 0/0\) o que é uma indeterminação.
Na verdade o sistema de equações montado não contempla esta solução pois a 2a equação ficaria da forma: \[ 0 = 0 \sigma T_a^4, \] ou seja, qualquer valor de \(T_a\) resolve o problema. Uma atmosfera totalmente transparente não troca energias com o meio, logo ela pode ter qualquer temperatura!
Já a temperatura da superfície torna-se: \[ T_s^4 = \frac{1}{\sigma}(1-r_s)(1-a_c)E,\] como obtido no caso anterior do planeta sem atmosfera.
Casos Particulares
- Planeta com superfície preta (ondas curtas/visível), \(r_s=0\). Este planeta, além de já ser "negro" no infravermelho térmico (corpo-negro), ele é completamente preto no visível também. Ele será certamente mais quente do que sua versão não-preta.
As temperaturas tornam-se:
\[T_a^4 = \frac{a_c + a_l(1-a_c)}{a_l(2-a_l)}\frac{E}{\sigma}, \qquad T_s^4 = \frac{2-a_c}{2-a_l}\frac{E}{\sigma}.\]
As temperaturas apenas dependem de \(E\), do coeficiente de absorpção de ondas curtas e de ondas longas.
- Se \(a_c=a_l=a \quad \rightarrow \quad T_a^4=E/\sigma = T_s^4\), logo ele é isotérmico.
- Se \(a_c>a_l\), mais espalhamento atmosférico do que absorção, \(T_s\) será menor que no caso isotérmico.
- Se \(a_c<a_l\), menos espalhamento do que absorpção, \(T_s\) será maior que no caso isotérmico.
- Em ambos os casos \(T_a\) se comporta opostamente.
Casos Particulares
- O Planeta Terra (\(r_s\approx 0,3\)) mas sem núvens (\(a_c\approx 0,2\) e \(a_l \approx 0,8\)).
\[ T_a = 257K = -15C,\qquad T_s = 288K = 15C.\]
- O Planeta Terra (\(r_s\approx 0,3\)) mas com núvens (\(a_c\approx 0,7\) e \(a_l \approx 1,0\)).
\[ T_a = 277K = 4C,\qquad T_s = 291K = 18C.\] Aqui o efeito estufa está caracterizado pelo aumento do espalhamento atmosférico e pela absorção total das ondas longas.
Exercícios:
- Calcule os valores para os dois casos do Planeta Terra e confirme os resultacos acima.
- Varie a reflectância em ±10% do valor aceito e recalcule os valores de \(T_a\) e \(T_s\) para o caso Terra com núvens.
- Estime a temperatura de equilíbrio de um planeta cuja atmosfera absorva toda a radiação de ondas curtas, mas não absorva nada da radiação de ondas longas. Aqui calcule \(T_s\) primeiro. Ao calcular \(T_a\) veja o que ocorre. Pense que se \(a_l=0\) temos que a atmosfera não emite energia térmica com o meio.
- Faça o mesmo para um planeta cuja atmosfera absorva toda a radiação de ondas longas, mas não absorva radiação de ondas curtas. (Este seria um caso parecido com um planeta denso e quente como Vênus). Calcule \(T_s\) e \(T_a\)
Taxa de aquecimento/resfrieament radiativo
Considere uma camada atmosférica com:
- Ela tem base na altura \(z_1\) e topo na altura \(z_2\).
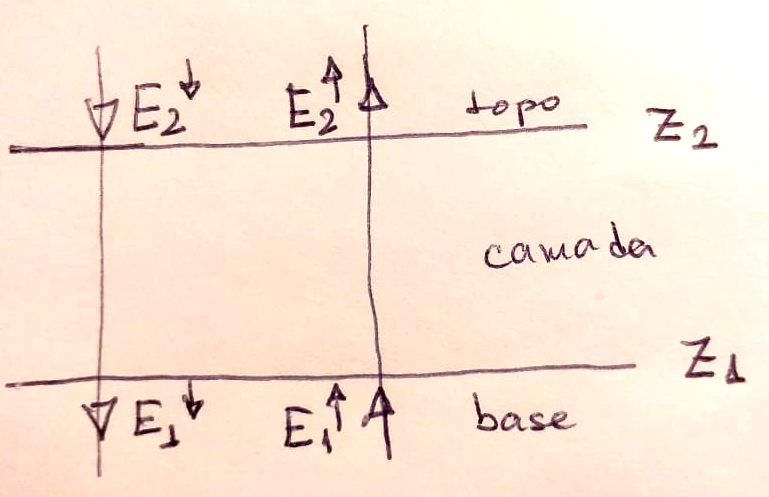
- A radiação que entra por cima (no topo, \(z_2\)) é: \(E(z_2)^{\downarrow}\).
- A radiação que sai por cima (na base, \(z_1\)) é: \(E(z_1)^{\downarrow}\).
- A radiação que entra de baixo (na base \(z_1\)) é: \(E(z_1)^{\uparrow}\).
- A radiação que sai de baixo (no topo, \(z_2\)) é: \(E(z_2)^{\uparrow}\).
Taxa de aquecimento/resfrieament radiativo
A conservação de energia nessa camada atmosférica é dada por: \[\Delta E = E_\text{entra} - E_\text{sai} = E(z_2)^{\downarrow} + E(z_1)^{\uparrow} - E(z_1)^{\downarrow} - E(z_2)^{\uparrow} = \] \[ = (E(z_2)^{\downarrow} - E(z_1)^{\downarrow}) - (E(z_2)^{\uparrow} - E(z_1)^{\uparrow}) = \] \[ = \Delta E^{\downarrow} - \Delta E^{\uparrow}.\]
Taxa de aquecimento/resfrieament radiativo
No Equilíbrio: \[\Delta E^{\downarrow} = \Delta E^{\uparrow},\] mas quando não estamos no equilíbrio, há mudança da energia interna.
1a. lei da Termodinâmica: \[ \Delta E_\text{int} = \Delta Q + \Delta W.\]
O termo \(\Delta W\) é o trabalho realizado sobre o sistema. Trabalho é \(F.x\), logo tem que haver deslocamento. Se a atmosfera for considerada estático (não aumentar ou diminuir de volume) então \(\Delta W = 0\), logo: \[ \Delta E_\text{int} = \Delta Q.\]
- A relação entre calor \(Q\) e a temperatura do material \(T\) é dada pela fórmula do calor específico:
\[ \Delta E_\text{int} = \Delta Q = m c_p \Delta T.\]
Taxa de aquecimento/resfrieament radiativo
A massa é dada por \(m = V\rho = A\Delta z \rho\), onde \(A\) é a área da camada. Dividindo tudo por \(A\), transformamos \(E\) de J para J/m²: \[\Delta E_\text{int} = \Delta z \rho c_p \Delta T.\]
Para termos a variação no tempo e irmos de energia para fluxo de energia, precisamos dividir por um intervalo de tempo \(\Delta t\): \[\Delta I_\text{int} = \Delta z \rho c_p \frac{\Delta T}{\Delta t},\]
Taxa de aquecimento/resfrieament radiativo
\[\Delta I_\text{int} = \Delta z \rho c_p \frac{\Delta T}{\Delta t},\] onde \(I\) é agora em W/m², e é a mudança do fluxo radiante entre o topo e a base da camada. Finalmente, dividindo tudo por \(\Delta z\), temos:
\[ \frac{dI}{dz} = \rho c_p \frac{dT}{dt}.\]
O termo \(\frac{dI}{dz}\) representa o Divergente da radiância: \[\vv{\nabla}\cdot \vv{I} = \rho c_p \frac{dT}{dt},\] e na verdade é igual a equação da propagação do calor.
Exercício
- Considere o planeta do problema 4 acima, completamente opaca para as ondas longas (\(a_l=1\)), e inteiramente transparente para as ondas curtas (\(a_c=0\)). Sua superfície é de um corpo-negro (\(a_s=\epsilon=1\)) e tem reflectância \(r_s\).
- Expresse os valores de \(T_a\) e \(T_s\) no equilíbrio.
- Agora, mude a reflectancia para \(r_s=1\), qual seria o impácto na temperatura de equilíbrio?
Balanço Radiativo na Superfície
Na superfície ocorrem trocas de energia tanto radiativas quanto não-radiativas.
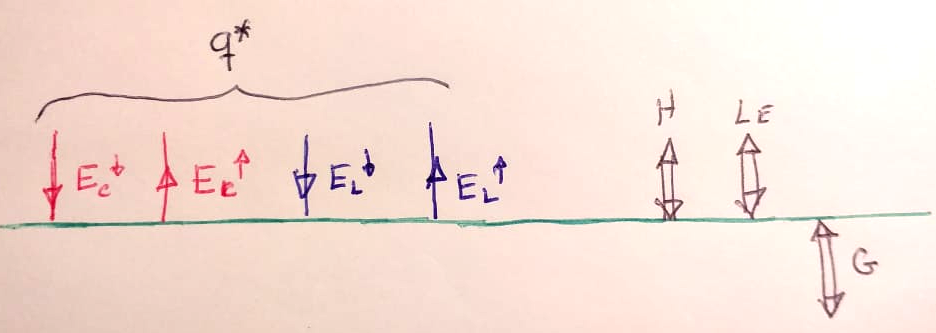
- O saldo de energia radiativa: \(q* = E_c^{\downarrow} + E_l^{\downarrow} - E_c^\uparrow - E_l^\uparrow.\)
- A troca turbulenta de calor sensível (ar quente/frio): \(H\).
- A troca turbulenta de calor latente (umidade que transforma em vapor e vice-versa): \(L_e\).
- O calor tracado por condução entre a superfície e o subsolo: \(G\).
Há ainda outras formas de troca de energia, vento, corpos aquáticos, ..., mas esses são os básicos.
Balanço Radiativo na Superfície
A equação do balanço radiativo fica na forma:
\[ q* = H + L_e + G.\]
Balanço Radiativo na Superfície
As variáveis \(H\), \(L_e\) e \(G\) são derivadas das condições meteorológicas (temperatura, umidade, ventos, etc...) e de propriedades do solo (capacidade térmica da superfície, evapotranspiração, etc...).
Já o valor do saldo radiativo \(q*\) é normalmente medido empiricamente atraves de radiômetros:
- Ondas curtas, virado para cima: mede a radiação solar incidente.
- Ondas curtas, virado para baixo: mede a radiação solar refletida.
- Ondas longas, virado para cima: mede a radiação térmica da atmosfera incidente.
- Ondas longas, virado para baixo: mede a radiação térmica emitida pelo solo.
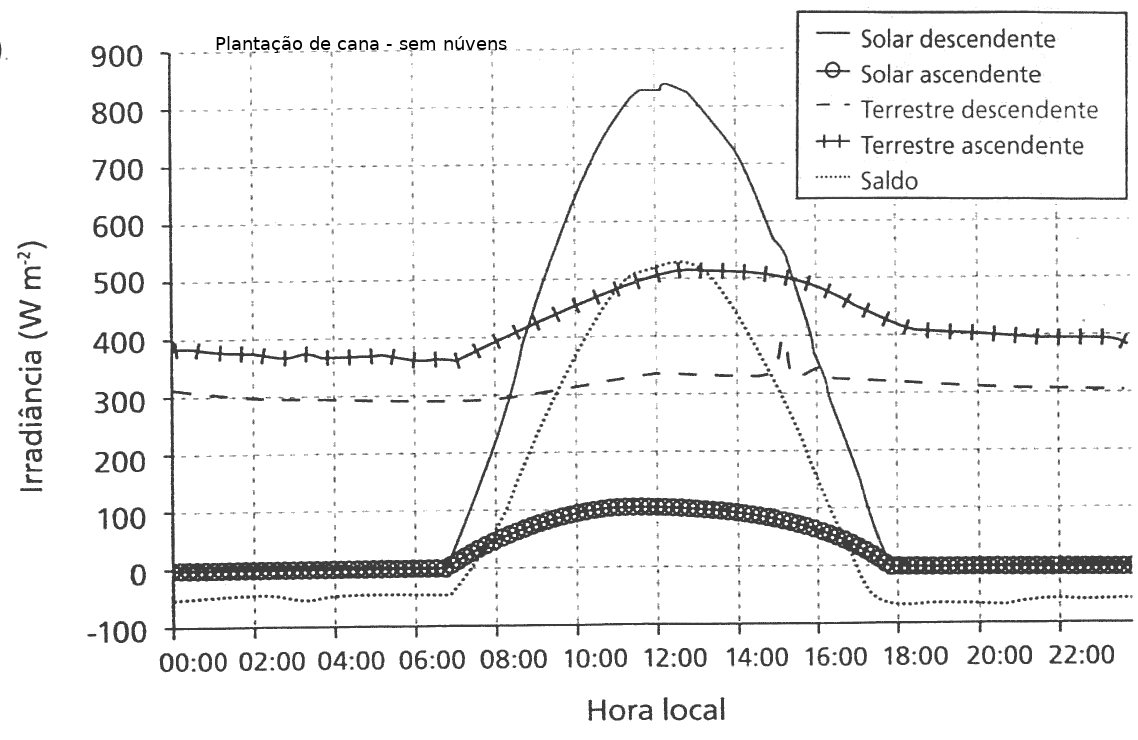
Fazenda de cana - SP - Agosto - céu claro:
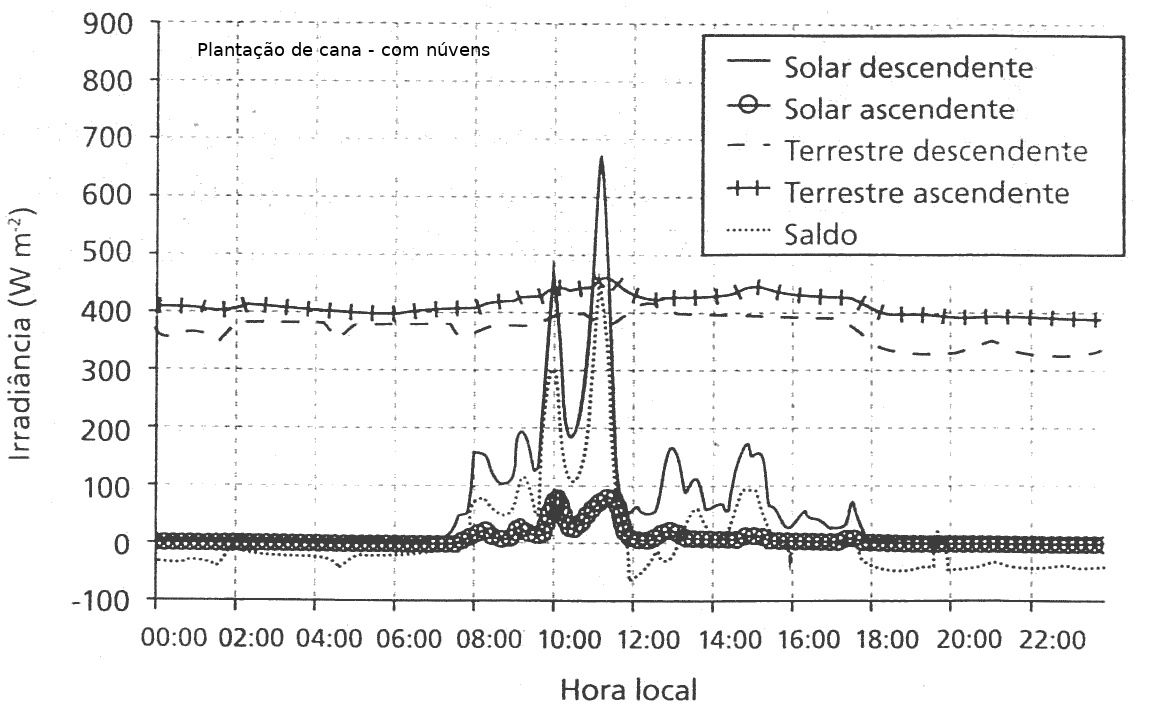
Fazenda de cana - SP - Agosto - céu nublado:
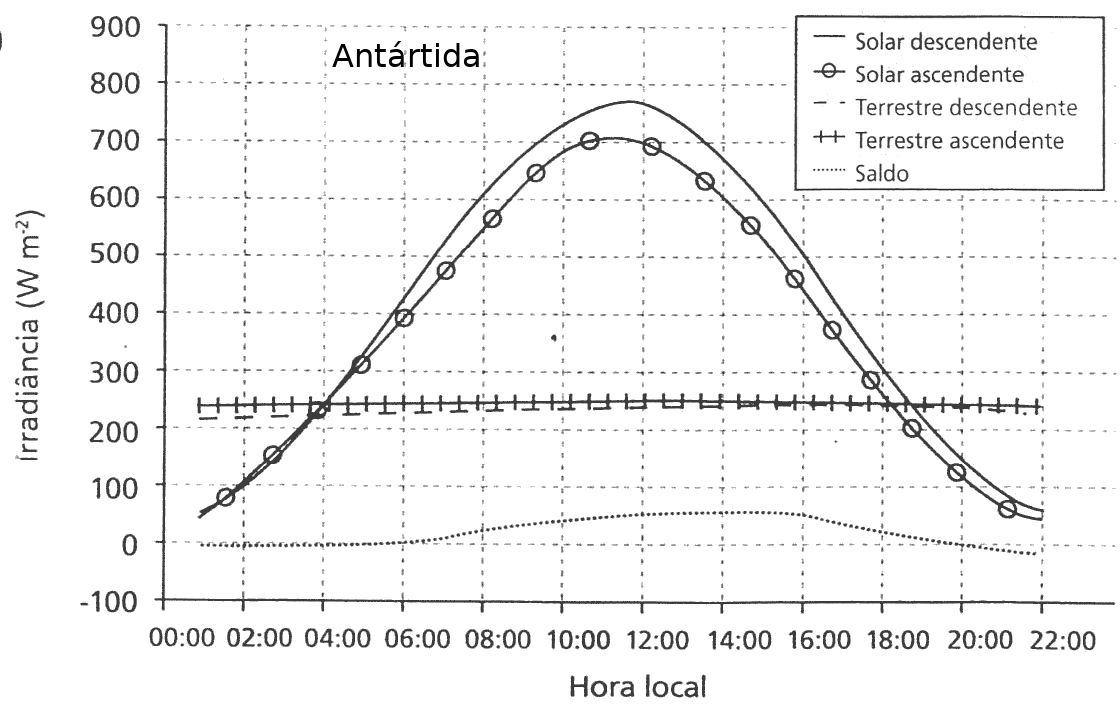
Simulado da Antártida:
Exercícios
- Qual a importância do albedo da superfície no balanço radiativo da superfície (saldo)? Para isso compare a Fig. da Antártida e da Fazenda de cana em dia nublado, e note que, a irradiância solar na Antártida é maior que na fazenda. Que componente do balanço é afetado?
- Como a cobertura de núvens modifica o balano de radiação em superfície? Elas são responsáveis por quais interações com a radiação solar? E com terrestre?



 * Unidade: steroradiano (sr).
* Unidade: steroradiano (sr).










 \[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]
\[S=\int k_a(\nu) d\nu\qquad \int f(\nu-\nu_0)d\nu = 1.\]